Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 15
- Tente encontrar uma janela retangular apropriada para .
- Você precisa de mais de uma janela? Por quê?
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão deu pra gente a função
E, no item a), pediu para que a gente encontrasse uma janela retangular apropriada para ela.
Isso significa que precisaremos entender como é o gráfico dessa função para determinar em que região seu comportamento pode ser melhor representado.
Além disso, no item b), a questão pede para que a gente diga se será necessária mais de uma janela para essa função e justifique nossa resposta.
E novamente isso dependerá do comportamento da função.
Vamos então entender melhor quem ela é para resolver esse exercício. Vem comigo que te ajudo com isso.
Passo 2
Vamos tentar analisar a expressão para nos dar uma ideia da janela mais adequada, ok?
Nossa função é:
Que pode ser escrita com:
Repara que a função é formada por uma divisão entre duas funções de tipos diferente.
Uma é a função polinomial
E a outra é a função exponencial
Como está no denominado, podemos determinar uma de suas raízes como sendo
Com isso, uma boa janela seria aquela que mostrasse a raiz da função. Então uma boa ideia seria uma janela e
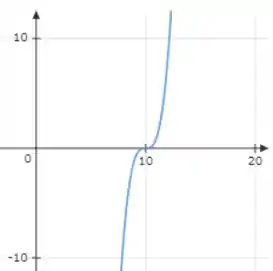
Porém, o denominador faz uma alteração bem importante em nossa função, uma vez que para valores de próximos a zero, a função tenderá para e para valores muito grandes de a função tenderá a zero.
E nossa curva se torna na mesma janela:
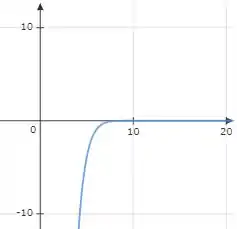
Passo 3
No item b) precisamos dizer se será necessária mais de uma janela.
A resposta é sim, pois com uma única janela não fica suficientemente claro a quão próxima das a função se está de um determinado valor.
O ideal seria ter uma janela com próximo de zero e outra com
Resposta
a) Janela e
b) Uma só janela não seria suficiente devido ao comportamento da função com próximo de zero e