Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 3

Se f x = e x - 2 ,   0 ≤ x ≤ 2 ,   calcule a soma de Rieman com n = 4 correta até a 6 casa decimal, tomando como pontos amostrais os pontos médios. O que representa a soma de Rieman? Ilustre com um diagrama.

Passo 1

Olá, meu caro amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui iremos utilizar a soma de Rieman para resolver essa atividade.

Para começar, vamos rever a fórmula da soma de Rieman,

S =   ∑ i = 1 4 f x i * Δ x =    

Com Δ x = b - a n .  

No nosso caso, x i * = x i - = 1 2 x i - 1 + x i e Δ x = 2 - 0 4 = 1 2 .

x l - = p o n t o   a m o s t r a l   m é d i o

n   é   o   n ú m e r o   d e   s u b i n t e r v a l o s .

Δ x = c o m p r i m e n t o   d o   i - é s i m o   s u b i n t e r v a l o

a \ b = i n t e r v a l o   [ a , b ]

Passo 2

Vamos ao digrama? Importante analisar ele antes de começarmos a resolução propriamente dita.

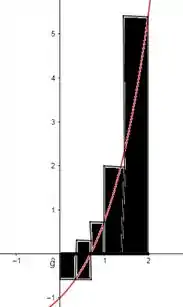
A soma representa a soma das áreas dos três retângulos acima do eixo x , menos a área dos retângulos abaixo do eixo, x ,   ou seja, a área liquida do retângulo em relação ao eixo x .

Substituindo na fórmula, temos que:

S = ∑ i = 1 4 f x i - Δ x =   Δ x     f x 1 - +     f x 2 - +   f x 3 - +   f x 4 -

A extensão do intervalo onde observamos x   ([0,2]) é 2. Com n = 4   , dividimos 2 por 4, o que nos dá 4 retângulos com larguras de 0,5 e alturas determinadas pela função f x no ponto médio de cada retângulo. Os pontos iniciais dos retângulos são 0, 0,5, 1 e 1,5. Isso significa que a altura para o primeiro retângulo é determinada como f 0,25 , pois 0,25 é o ponto médio de 0 e 0,5.

Substituindo as informações,

  Δ x     f x 1 - +     f x 2 - +   f x 3 - +   f x 4 - =   1 2 f 1 4 - +     f 3 4 +   f 5 4 - +   f 7 4  

Aplicando a função,

1 2 f 1 4 ¯ +     f 3 4 +   f 5 4 ¯ +   f 7 4 =

1 2 e 1 4 - 2 +   e 3 4 - 2 +   e 5 4 - 2 +   e 7 4 - 2 =

Resolvendo as contas,

S ≈ 2 ,   322986  

Resposta

S ≈ 2 ,   322986  

A soma representa a soma das áreas dos três retângulos acima do eixo x , menos a área dos retângulos abaixo do eixo, x ,   ou seja, a área liquida do retângulo em relação ao eixo x .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) de a Regra de Simpson para aproximar a integral dada com o valor n especificado. ∫ 0 2 1 1 + x 6 ,n = 8
Depois de uma injeção de 5,5 mg de contraste, as leituras de concentração do contraste, em mg/L, a intervalos de dois segundos, são mostradas na tabela. Use a Regra de Simpson para estimar a capacidad
Com uma calculadora programável ou computador(veja as instruções para exercício 9 da seção 5.1) , calcule as somas de Rieman esquerda e direita par aa função f x = x x + 1 no intervalo [ 0,2 ] , com n
Se você tiver um sca que possa calcular aproximações usando pontos médios e esboçar os retângulos correspodnentes , verifique n=10 e n= 20
Use a Definição 2 para achar uma expressão para a área sob o gráfico de como um limite. Não calcule o limite. f x = x 4 ,1 ≤ x ≤ 16