Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 18
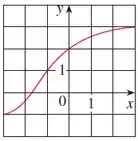
É dado o gráfico de .
(a) Por que é injetora?
(b) Determine o domínio e a imagem de
(c) Qual o valor de ?
(d) Obtenha uma estimativa para o valor de .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu o gráfico de uma função e pediu pra gente explicar porque essa função é injetora, determinar o domínio e o contradomínio da inversa dessa função, o valor de e obter uma estimativa para o valor de
O gráfico que ele nos deu foi esse aqui:
Pra dizer se essa é uma função injetora, precisamos usar o teste da reta horizontal. Desse modo, se ao traçarmos retas horizontais no gráfico da função, sem que nenhuma dessas retas intercepte mais de um ponto de , então, temos que é injetora.
Pra determinar o domínio e a imagem de , temos que lembrar que na função inversa, o domínio de se torna o contradomínio e o contradomínio se torna o domínio. Então, vamos olhar o gráfico e ver o intervalo de valores de (domínio) e de (imagem) que a função assume e inverter isso para encontrar as informações sobre a função inversa.
Depois, vamos determinar e usando o mesmo conceito e analisando o gráfico.
Vamos lá!
Passo 2
Vamos começar aplicando o teste da reta horizontal no gráfico da função:
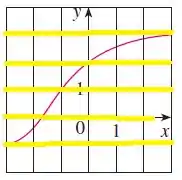
Observe que cada uma das retas em amarelo não tocam a função em mais de um ponto. Sendo assim, passa no teste da linha horizontal. Logo, é injetora.
Passo 3
Agora vamos analisar no gráfico os valores de e para os quais a função está definida e resolver a letra (b) da questão.
Observe que o domínio de compreende os valores de no intervalo . E que a imagem de está definida para os valores de no intervalo .
Então, pra função inversa, , vai ser o contrário. Assim, teremos:
Passo 4
Seguindo o mesmo raciocínio para encontrar na letra (c), vamos olhar no gráfico o valor de . Assim, obtemos:
E como a função inversa, , vai ser aquela que transforma de volta pra , vamos ter:
Passo 5
Da mesma forma, para resolver a letra (d), vamos analisar o gráfico no ponto , para encontrar uma estimativa para .
Observe que quando , temos . Sendo assim, a função inversa nesse ponto será:
Valeu, galera! Até a próxima! 😉
Resposta
(a) é injetora porque passa no teste da linha horizontal
(b) e
(c)
(d)