Dado o gráfico a seguir, responda as perguntas abaixo

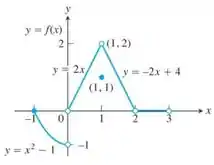
Para que novo valor deve ser alterada para remover a descontinuidade?

Temos aqui uma função super estranha. Para cada intervalo de nosso se comporta diferente. Mas mesmo assim podemos ter uma função continua. Basta que no ponto que queremos, o limite indo pela esquerda e pela direita sejam iguais. Em termos mais matemáticos seria algo do tipo

Queremos o ponto onde , se formos seguir essa logica, indo pela esquerda e pela direita, vamos seguir duas retas que se cruzam em . Então formalizando seria

Prontinho, precisamos apenas mover o ponto e nosso problema está resolvido. Essa foi rapidinha, não perde o ritmo, nos encontramos na próxima questão 😊