Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 9
Dado que , ilustre a Definição 6 encontrando os valores de que correspondam a
- .
Passo 1
Olá, meu nobre amigo. Estarei te ajudando a resolver essa atividade.
Aqui iremos utilizar da definição 6 para encontrar o para os valores de que queremos.
Abaixo temos a definição 6:
Basicamente queremos encontrar uma distância para qual dado o valor de no enunciado, nossa função seja maior que esse , e no nosso caso deveremos encontrar os deltas que sejam suficiente para nossa função ser maior que e .
Isso é a definição do limite infinito, que dado um número qualquer, a gente sempre conseguira ter ajustando a distância que nosso está de .
Passo 2
Letra a)
Vamos analisar o gráfico da nossa função, iremos buscar então a distância com ajuda do gráfico. Lembre-se, precisamos descobrir qual distância entre o valor que nesse caso é pois estamos nos aproximando de e . Anote aí, é o nosso da definição.
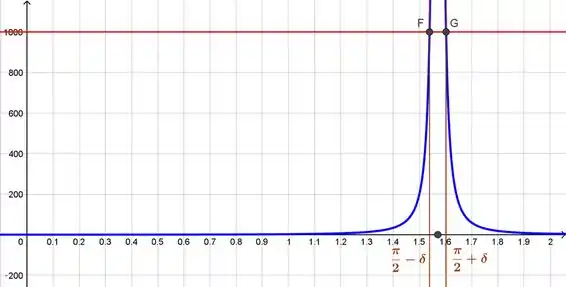
Buscamos posicionar as linhas verticais de modo que elas interceptem em , e a partir disso, iremos encontrar no eixo a distância
A distância disso de é
é simétrico em torno de , então há apenas um valor .
coordenada do ponto
coordenada do ponto . Então quando estamos chegando a mas estamos a uma distância de de , teremos então o nosso .
Passo 3
Letra b)
O pensamento para a letra b) é semelhante, porém agora teremos um diferente.
Vamos analisar o gráfico da nossa função, iremos buscar então a distância com ajuda do gráfico. Lembre-se, precisamos descobrir qual distância entre o valor que nesse caso é pois estamos nos aproximando de e . Anote aí, é o nosso da definição
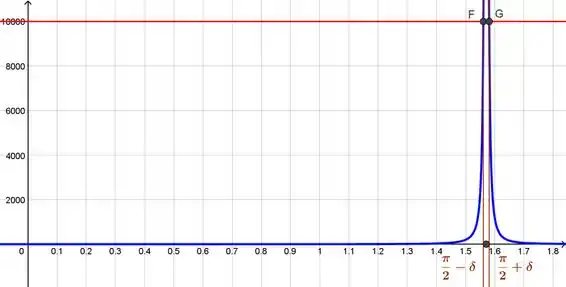
Buscamos posicionar as linhas verticais de modo que elas interceptem em , e a partir disso, iremos encontrar no eixo a distância
A distância disso de é
é simétrico em torno de , então há apenas um valor .
coordenada do ponto
coordenada do ponto . Então quando estamos chegando a mas estamos a uma distância de de , teremos então o nosso .