Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 34
Verifique, usando argumento geométricos, que a maior escolha possível para o para que se possa mostrar que é .
Passo 1
Oi galerinha do RA, bora resolver mais um juntinho?
Dado o problema:
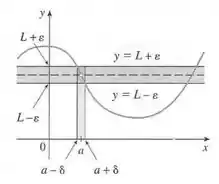
Queremos provar que para todo existe tal que se , então .
Entender a definição de limite: O limite
significa que quando se aproxima de 3, se aproxima de 9.
Manipulação algébrica: Vamos começar manipulando a expressão .
Podemos fatorar isso como , porque é um quadrinômio da forma
Passo 2
Visualização geométrica: Sabemos que representa a distância entre no eixo Assim, podemos pensar em como a distância entre no eixo x.
Estamos interessados em restringir essa distância para provar que é pequeno o suficiente.
Escolha estratégica de e Vamos escolher como a restrição para ou seja, queremos que
Substituição direta: Vamos substituir por na desigualdade
Escolha de Como queremos controlar a expressão podemos escolher de modo que seja restrito por alguma expressão envolvendo
Observamos que estará restrito se estiver restrito.
Então, podemos escolher de forma que esteja restrito por .
Passo 3
Testar limites especiais: Como pode ser 0, precisamos considerar limites pela direita e pela esquerda de
Finalização da prova: Vamos manipular a expressão de modo a restringi-la em termos de e
Então, podemos escolher como
Assim, para todo , se , então , o que prova que .
Resposta
Demonstração.