Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 2
- Use o gráfico de para encontrar um número tal que se então
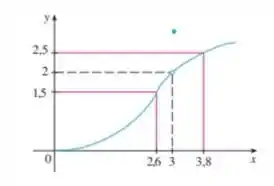
Passo 1
Olá, meu amigo. Vamos para mais uma resolução.
Aqui a gente tem a função e utilizando o gráfico de
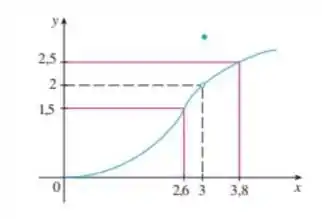
Vamos encontrar um tal que se então . Isso significa que precisamos encontrar uma distância entre e para que nossa função esteja a uma distância de . É isso que se trata o limite e sua definição.
Pra fazermos essa, temos que lembrarmos da definição de limite, olha só:
Se para todo número houver um número tal que:
Se então
Então, isso pode ser interpretado, como foi já comentado, como uma distância que tem de que faz com que nossa função esteja a uma distância do seu limite .
O que vamos fazer aqui é procurar essas distancias por meio do gráfico.
Passo 2
Como , podemos retirar o modulo e reescrever da seguinte forma:
Logo,
Analisando o gráfico, podemos ver que nesse intervalo de , temos:
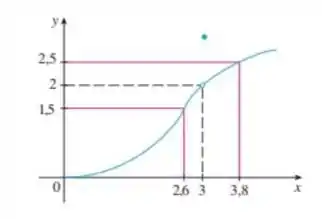
Para o , temos:
Novamente retirando o modulo,
Passo 3
Agora vamos trabalhar com as equações e .
1° caso:
Substituindo :
Então nosso intervalo fica o seguinte:
Isto é,
Como está dentro do nosso intervalo,
2° caso:
Então nosso intervalo fica o seguinte:
Isto é,
Esse valor de não serve, pois temos o está fora do intervalo, então ficamos com