Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 3.10 - Ex. 19
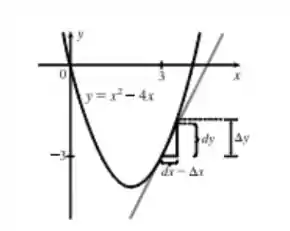
Dados e , calcule . Depois, mostre em um diagrama a reta tangente.
Passo 1
Fala aí pessoal, partiu resolver mais um problema de cálculo.
Nessa questão nos é dado que:
E temos que .
Nos é pedido para calcular e , sendo que:
Para calcular , que é uma variação em quando há uma variação em , podemos fazer:
E por fim para calcular , que é uma variação infinitesimal em quando há uma variação infinitesimal em , podemos fazer:
Passo 2
Sabemos que para calcular vamos ter que usar:
Agora, para achar vamos usar:
Precisamos da derivada dessa expressão que é:
Substituindo o por , temos:
Portanto,
Desenhando:
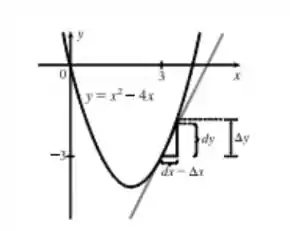
Resposta
Exercícios de Livros Relacionados
Uma flecha é lançada para cima com uma velocidade de 58m / s , e sua altura em metros após t segundos é dada por h = 58 t - 0,83 t 2 .Encontre a velocidade média durante os intervalos de tempo dados:
O ponto P 2 , ln 2 pertencente à curva y = ln x . Se Q é o ponto ( x , ln x ) , use a sua calculadora para determinar o coeficiente da reta secante P Q , com precisão de seis casas decimais, par
O deslocamento (em pés) de uma certa partícula movendo-se em linha reta é dado por s = t 3 6 .Encontre a velocidade média durante os períodos de tempo a seguir: i 1,3 i i 1,2 i i i 1 ,1,5 i v 1 ,1,1 E
A inclinação da reta tangente ao gráfico da função exponencial y = 2 x no ponto ( 0,1 ) é lim x → 0 ( 2 x - 1 ) x . Estime a inclinação até três casas decimais.
Uma bola é atirada no ar com uma velocidade de 40p é s / s é , e sua altura em pés após t segundos é dada por y = 40 t - 16 t 2 .Encontre a velocidade média para o período de tempo que começa quando t