Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.1 - Ex. 4
O ponto pertencente à curva
- Se é o ponto , use a sua calculadora para determinar o coeficiente da reta secante , com precisão de seis casas decimais, para os seguintes valores de
- Usando os resultados da parte , estime o valor da inclinação da reta tangente à curva no ponto .
- Use a inclinação obtida na parte para achar uma equação da reta tangente à curva em
- Faça uma figura utilizando duas retas secantes e a reta tangente.
Passo 1
Eaee, belezinha??? Bom... o enunciado nos diz que o ponto pertencente à curva
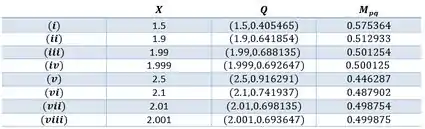
A partir desse dado, queremos determinar o coeficiente da reta secante (onde o ponto é ) com precisão de seis casas decimais, para os seguintes valores de :
Com isso, deveremos estimar o valor da inclinação da reta tangente à curva no ponto e sua equação.
Para resolvermos isso tudo é interessante lembrarmos que:
- Reta secante corta uma curva em dois ou mais pontos;
- Uma reta tangente toca a curva em um único ponto, proporcionando uma aproximação local da curva naquele ponto.
É interessante lembrarmos também que a equação de uma reta é dada por:
Onde são pontos conhecidos e é a inclinação da reta.
Agora bora lá!! 😉
Passo 2
Opa, bora lá! Como a questão foi bem direta, vamos partir para a resolução. Assim, o coeficiente da reta secante vai ser dado por:
Assim, para , temos:
Logo, o coeficiente para esse ponto é:
Assim, aplicando os demais valores dados no enunciado, obteremos a seguinte tabela:
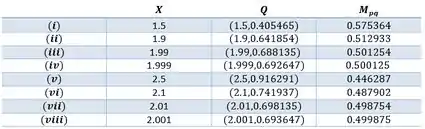
Percebe-se que a inclinação se aproxima de .
Passo 3
Com isso, nossa equação da reta vai ser dada por:
Passo 4
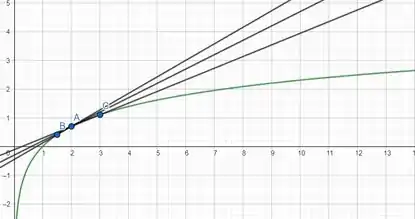
Plotando duas retas secantes e uma reta tangente vamos ter
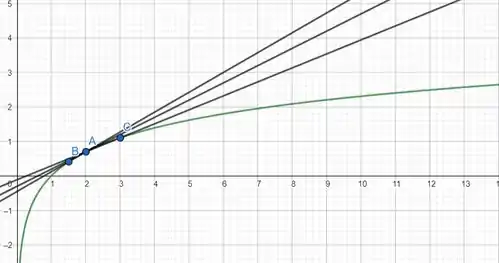
Prontinho!
Resposta
