Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.1 - Ex. 32

32.

(a) Deduza a identidade

sech ⁡ 2 x = sech 2 ⁡ x 1 + tanh 2 ⁡ x

(b) Use o resultado de (a) para calcular ∫ sech ⁡ x d x .

(c) Deduza a identidade

sech ⁡ x = 2 e 2 x e 2 x + 1

(d) Use o resultado de (c) para calcular ∫ sech ⁡ x d x .

(e) Explique por que as respostas de (b) e (d) são consistentes.

Passo 1

(a) Para deduzir a identidade, vamos partir de uma identidade mais simples para chegar na expressão desejada. A identidade é:

cosh ⁡ 2 x = cosh 2 ⁡ x + s e n h 2   x

Dividindo tudo por cosh 2 ⁡ x , temos:

cosh ⁡ 2 x cosh 2 ⁡ x = cosh 2 ⁡ x cosh 2 ⁡ x + s e n h 2   x cosh 2 ⁡ x ↔ cosh ⁡ 2 x . sech 2 ⁡ x = 1 + tanh 2 ⁡ x

Agora basta manipular algebricamente:

cosh ⁡ 2 x . sech 2 ⁡ x = 1 + tanh 2 ⁡ x ↔ cosh ⁡ 2 x = 1 + tanh 2 ⁡ x sech 2 ⁡ x

Invertendo ambos os termos:

1 cosh ⁡ 2 x = 1 1 + tanh 2 ⁡ x sech 2 ⁡ x ↔ sech ⁡ x = sech 2 ⁡ x 1 + tanh 2 ⁡ x

Como queríamos deduzir.

Passo 2

(b) Para resolver a integral, vamos precisar apenas de substituições simples. Como a identade vale apenas para sech ⁡ 2 t , devemos fazer a substitução x = 2 t ↔ d x = 2 d t , dai temos:

∫ sech ⁡ x d x = 2 ∫ sech ⁡ 2 t d t = 2 ∫ sech 2 ⁡ t 1 + tanh 2 ⁡ t d t

Agora falta a ultima substituição, que também é simples. Vamos usar o fato de que d ( tanh ⁡ t ) d t = sech 2 ⁡ t . Sendo assim, façamos u = tanh ⁡ t ↔ d u = sech 2 ⁡ t d t , daí obtemos:

2 ∫ d u 1 + u 2 = 2 arctan ⁡ u + C

Voltando a variável t , temos:

2 ∫ sech ⁡ 2 t d t = 2 arctan ⁡ ( tanh ⁡ t ) + C

Voltando à variável x:

∫ sech ⁡ x d x = 2 arctan ⁡ ( tanh ⁡ x 2 ) + C

Passo 3

(c) Para deduzir a identidade, vamos apenas aplicar a definição, desta forma:

cosh ⁡ x = e x + e - x 2 ↔ sech ⁡ x = 1 cosh ⁡ x = 2 e x + e - x

Agora basta apenas fatorar o e - x , daí temos:

sech ⁡ x = 2 e - x ( e x e - x + 1 ) = 2 e x e 2 x + 1

Passo 4

(d) Para calcular a integral usando basta apenas fazer u = e x ↔ d u = e x d x , daí obtemos:

∫ sech ⁡ x d x = ∫ 2 e x e 2 x + 1 d x = ∫ 2 u 2 + 1 d u = 2 arctan ⁡ u + C

Voltando a variável x , temos:

∫ sech ⁡ x d x = 2 arctan ⁡ ( e x ) + C

Passo 5

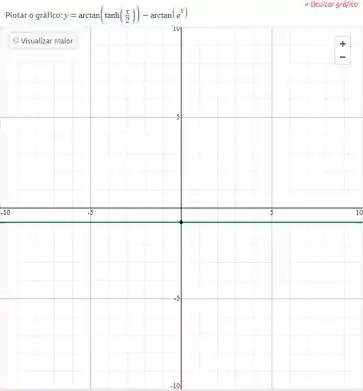
(e) Apesar de funções diferentes terem sido obtidas a partir de cada uma das identidades, ambas são equivalentes e igualmente verdadeiras. Todas as manipulações algébricas utilizadas tanto em (a) quanto em (c) para obter as identidades são formas equivalentes das expressões de onde partimos, e como as técnicas de integração empregadas resolvem de fato as integrais, significa que apesar de expressões diferentes, são funções iguais a menos de uma constante C.A critério de curiosidade, veja o gráfico da diferença entre as funções e veja como essa diferença resulta em uma constante, representada pela reta azul no gráfico (no caso: C = - π 4 ) .

Resposta

a)Demonstração acima.

b)   2 arctan ⁡ ( tanh ⁡ x 2 ) + C

c)Demonstração acima.

d)   2 arctan ⁡ ( e x ) + C

e)Explicação acima.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Tabela de Integrais para calcular a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em (a). ∫ x 2
Use a Tabela de Integrais para calcular a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em (a). ∫ e -
Use a Tabela de Integrais para calcular a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em (a). ∫ sen
Use a Tabela de Integrais para calcular a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em (a). ∫ 1 x
Use a Tabela de Integrais para calcular a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em (a). ∫ sen