Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.6 - Ex. 14

  1. Use a Tabela de Integrais para calcular a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral e, então, confirme que o resultado é equivalente ao que foi obtido em (a).

∫ 1 x 2 x 2 - 2 d x

Passo 1

Conhecemos a nossa integral:

∫ 1 x 2 x 2 - 2 d x

O exercício requer que usemos a tabela de integral para realizar o cálculo. Usaremos a fórmula que diz que :

∫ 1 u 2 u 2 ± a 2 d u = ±   u 2 ± a 2 a 2 u + C

Passo 2

  1. Usando a fórmula dada, chamaremos:

u = x

a 2 = 2

Se :

∫ 1 u 2 u 2 ± a 2 d u = ±   u 2 ± a 2 a 2 u + C

Substituindo na fórmula, temos: ∫ 1 x 2 x 2 - 2 d u =   x 2 - 2 2 x + C

Passo 3

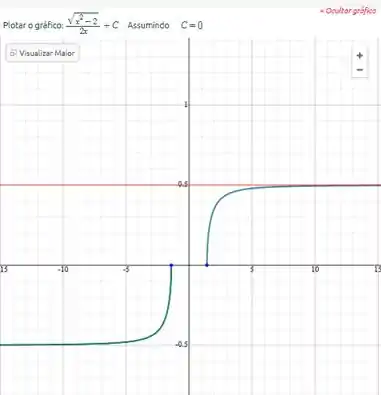
Utilizando ferramentas de resolução de integral online (pode-se usar o symbolab, Wolfram alpha). Colocando a fórmula dada, no programa:

Resposta

∫ 1 x 2 x 2 - 2 d u =   x 2 - 2 2 x + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola é jogada verticalmente para cima a partir de uma altura de s 0 metros com velocidade inicial de v 0 m/s. Se ela for pega na altura s 0 , determine sua velocidade média no ar usando o modelo d
Use as desigualdades (12), (13) e (14) da Seção 7.7 para encontrar cotas superiores para os erros nas partes (a), (b) e (c) dos exercícios indicados.Exercício 41.
Use as desigualdades (12), (13) e (14) da Seção 7.7 para encontrar um número n de subintervalos para (a) a aproximação pelo ponto médio M n , (b) a aproximação trapezoidal T n e (c) a aproximação S n
Use as desigualdades (12), (13) e (14) da Seção 7.7 para encontrar um número n de subintervalos para (a) a aproximação pelo ponto médio M n , (b) a aproximação trapezoidal T n e (c) a aproximação S n
Use as desigualdades (12), (13) e (14) da Seção 7.7 para encontrar cotas superiores para os erros nas partes (a), (b) e (c) dos exercícios indicados.Exercício 42.