Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 43
Use a Fórmula 10 para fazer o gráfico das funções dadas em uma mesma tela. Como se relacionam esses gráfico?
, , ,
Passo 1
E aí, tudo bem?! O enunciado nos dá as funções:
Temos que fazer o gráfico de todas essas curvas na mesma tela. Pra isso a gente vai precisar que todos esses logaritmos estejam na mesma base. E é aí que a fórmula do livro entra. Temos que:
Esse problema tem aquele sinalizinho rosa no lado do número da questão. Isso significa que podemos usar um software pra plotar os gráficos!
Passo 2
Vamos começar fazendo as mudanças de base nas curvas:
Trazendo a fórmula pra perto:
Aplicando:
Passo 3
Agora a gente plota as curvas:
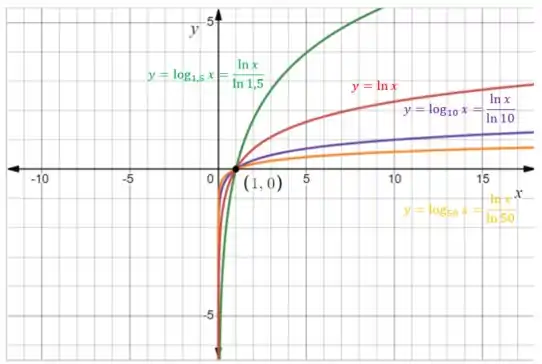
Aqui podemos ver que quanto maior o denominador, mais devagar a função cresce!
Repara também que todas as curvas passam pelo ponto , isso porque:
Pois:
Assim, independentemente do valor do denominador, a função sempre vai cruzar o eixo em , desde que não tenha nenhuma constante sendo adicionada ou subtraída, o que deslocaria a função para cima ou para baixo, certo? É isso!
Resposta
