Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 44
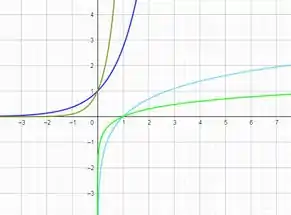
Use a Fórmula 10 para fazer o gráfico das funções dadas em uma mesma tela. Como se relacionam esses gráfico?
,, ,
Passo 1
Bom, a fórmula 10 é, na real, a fórmula da mudança de base do logaritmo:
Ao invés do logaritmo natural, poderíamos usar um logaritmo com uma outra base, desde que seja a mesma base para o numerador e para o denominador. Vamos usar o logaritmo natural porque temos a tabela de valores, e fica mais fácil o cálculo então.
Passo 2
Colocando as funções nas fórmulas, temos:
Aqui, para calcular o valor de podemos usar manipulação dos números, utilizando as propriedades dos logaritmos, ou utilizar uma calculadora, depende da precisão que o exercícios nos pede. Como queremos o gráfico dessa função apenas, podemos fazer um arredondamento, utilizando apenas a tabela do logaritmo natural:
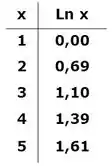
Assim:
Assim, fica fácil substituir uns valores de e descobrir alguns pontos. Depois é só ligar pensando no “molde” da função do logaritmo.
Passo 3
Beleza, agora que temos as nossas funções, podemos plotar elas em um mesmo gráfico, como o pedido:
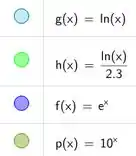
Aqui, podemos ver que as funções e são simétricas em relação à bissetriz, reta .
O mesmo acontece com e .
Isso indica que as funções são inversas!
Resposta
As funções são inversas.
