Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 16
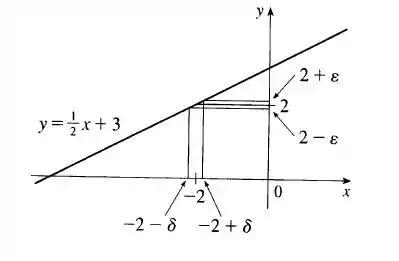
Demonstre cada afirmação usando a definição , de limite e ilustre com um diagrama como o da Figura 9.
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui iremos utilizar da definição de limites para resolver essa atividade.
A definição diz que:
Quando para todo número , existe um número tal que: se então .
Passo 2
Dado que , nós precisamos achar , tal que se:
Então temos que:
Vamos agora simplificar isso:
O que nos mostra que se:
Então:
Passo 3
Isso nos dá que se nós escolhermos , e substituirmos seu valor, temos que
Portanto, temos o limite
pelo limite da definição.
Passo 4
Aqui temos o diagrama:
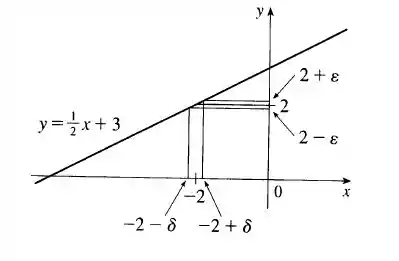
Resposta
Exercícios de Livros Relacionados
Calcule e justifique: lim x → 10 5
Calcule e justifique: lim x → - 1 - x 2 - 2 x + 3
Calcule e justifique: lim x → - 3 x 3
Calcule. lim x → 0 ⁺ ln x ⁺
Calcule. lim x → + ∞ log 3 x