Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.2 - Ex. 4a
Calcule.
Passo 1
Oiee. Bora ver essa questãozinha delícia!!! Para calcular esse limite vamos usar essa informação aqui:
Com .
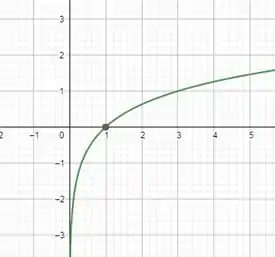
Veja bem, a regra diz que o limite do log de na base vai para o infinito quando o valor de vai crescendo para o . Mas pra isso fazer mais sentido pra gente podemos perceber o comportamente do limite atribuindo valores a e analisando seus valores na função logarítmica:
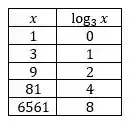
Viu que a menida que o foi crescendo, os valores o log também foram? Devagarinho, mas foram. E irão para todo o sempre, até o infinito.
Assim, vemos que a medida que cresce para mais infinito, também cresce para mais infinito também, assim:
Uma forma de visualizar essa tendência é através do gráfico:
Resposta
Exercícios de Livros Relacionados
Calcule o limite abaixo utilizando as propriedades de Limites. lim t → 2 t 2 - 5 t + 6 t - 2
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → π 2 [ 2s e nx - cos x + c o t gx ]
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → 2 2 x 2 - x 3 x
Calcule o limite abaixo utilizando as propriedades de Limites. lim x → 1 x 2 - 1 x - 1
Calcule o limite abaixo utilizando as propriedades de Limites. lim t → 2 t + 3 t + 2