Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 60
Demonstre que a equação tem pelo menos uma raiz real. Use sua ferramenta gráfica para encontrar a raiz correta até a terceira casa decimal.
Passo 1
Bom galera, nesse exercício queremos provar que a equação apresentada possui pelo menos uma raiz real e depois encontrar graficamente essa raiz.
Para isso, iremos utilizar o Teorema do Valor Intermediário. Nossa função é uma função polinomial com uma , e tanto a função trigonométrica quanto a função polinomial são funções contínuas.
Dessa forma, nossa função é contínua para qualquer intervalo a nossa escolha. Considerando o intervalo , iremos substituir os valores do intervalo na nossa função.
Vamos antes de iniciarmos a resolução dar uma olhada no que diz o Teorema do Valor Intermediário.
Passo 2
Temos a nossa equação:
Aplicando
Aplicando
Como , então, pelo Teorema do Valor Intermediário, no intervalo há um número tal que . bAssim, nossa função possui uma raiz dentro desse intervalo como queremos provar.
Passo 3
Com ajuda do GeoGebra iremos criar os gráficos que queremos:
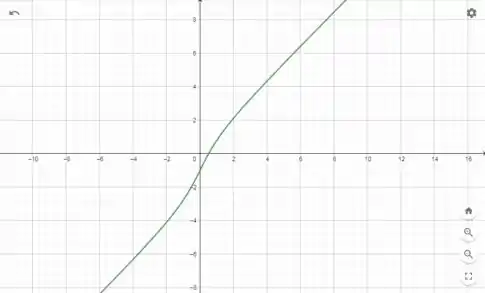
Dando um Zoom:
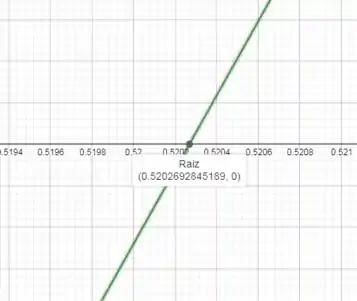
Aproximando a imagem da raiz, podemos ver que com três casas de precisão a raiz está em .
Resposta
A raiz da função se encontra em .