Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 71

Demonstre que a função

f (x) = {[[x^4 s e n ((1)/(x)) s e x != 0],[0 s e x = 0]])

É contínua em (- oo , oo) .

Passo 1

Fala aí, pessoal! 😎

Nesse problema temos que provar que a função

f (x) = {[[x^4 s e n ((1)/(x)) s e x != 0],[0 s e x = 0]])

É contínua em todo x in R .

Tem ideia de como fazemos isso? 😬

Nossa função é composta por um polinômio e um seno. O seno é uma função periódica e contínua em todos os pontos. E os polinômios também são contínuos em todos os pontos.

Então o único ponto em que a nossa função pode não ser contínua é o ponto x = 0 , pois temos o denominador não pode ser nulo, então nesse ponto, a expressão x^4 s e n ((1)/(x)) não está definida.

Passo 2

Porém, por definição da questão, nossa função f (x) = 0 quando x = 0 . Então pra que a função seja contínua em x = 0 , precisamos que:

underset(x -> 0)(lim) x^4 s e n ((1)/(x)) = f (0) = 0

Então bora calcular esse limite!

Pra isso vamos calcular o limite de x^4 s e n ((1)/(x)) para x -> 0

underset(x -> 0)(lim) x^4 s e n ((1)/(x))

Pra usar o teorema do confronto,

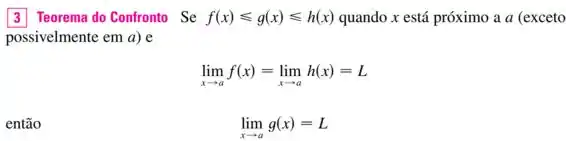vamos lembrar do intervalo de existência do seno:

- 1 <= s e n ((1)/(x)) <= 1

Multiplicando todos os lados por x^4 :

- x^4 <= x^4 s e n ((1)/(x)) <= x^4

E agora calculando os limites desses lados, temos:

underset(x -> 0)(lim) - x^4 <= underset(x -> 0)(lim) x^4 s e n ((1)/(x)) <= underset(x -> 0)(lim) x^4

0 <= underset(x -> 0)(lim) x^4 s e n ((1)/(x)) <= 0

Portanto, temos:

underset(x -> 0)(lim) x^4 s e n ((1)/(x)) = 0

Logo vemos que f é sim continua em todo domínio.

E aí! o que achou? Responde Aí! 😬

Resposta

A função f ( x ) é contínua no intervalo, como queremos provar.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o domínio da função e diga se é contínua nos intervalos: f r = r + 3 r 2 - 4 Intervalos: 0,4 ; - 2,2 ; - ∞ , - 2 ; 2 , + ∞ ; - 4,4 ; ( - 2,2 ]
Defina f o g e determine os números nos quais f o g seja contínua, sendo: f x = xeg x = x 2 + 4
Ache o domínio da função e diga se é contínua nos intervalos: f x = 2 x + 5 Intervalos: 3,7 ; - 6,4 ; - ∞ , 0 ; - 5 , + ∞ ; - 5 , + ∞ ; [ - 10 , - 5 )
Ache o domínio da função e diga se é contínua nos intervalos: f t = t t 2 - 1 Intervalos: 0,1 ; - 1,1 ; 0,1 ; - 1,0 ; ( - ∞ , - 1 ] ; ( 1 , + ∞ )
Ache o domínio da função e diga se é contínua nos intervalos: h x = 2 x - 3s ex- 2 x - 5s e - 2 ≤ x ≤ 1 3 - xs ex1 Intervalos: - ∞ , 1 ; - 2 , + ∞ ; - 2,1 ; - 2,1 ; [ - 2,1 ]