Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 43
Demonstre que
Passo 1
Olá, meu amigo, Yuri aqui e eu estarei lhe ajudando na resolução desta atividade.
O enunciado pede para usarmos a definição de limite para demonstrar que o limite de ‘explode’ para quando .
Normalmente quando o enunciado pede para que nós demonstremos algo ele quer dizer para que façamos isso pelo método formal matemático, aqui iremos fazer tanto de uma forma lúdica, utilizando o gráfico, quanto da forma mais matemática, utilizando a definição de limites.
Abaixo você ver o gráfico da função :
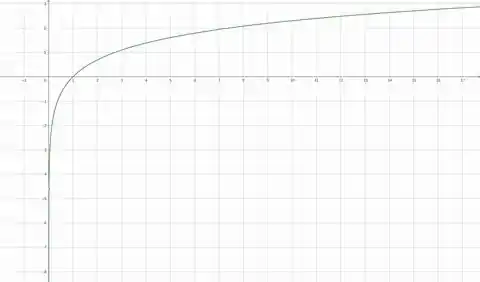
Vou dar um zoom nesse grafico para que possamos observar o comportamento da função quando nos aproximamos de , pela direita, pois é isso que significa o .
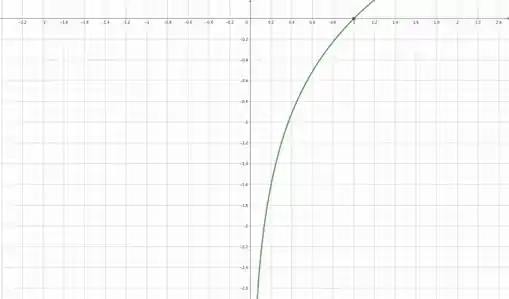
O que podemos observar é que a medida que vamos ficando mais perto de 0, maiores são os valores de , tão grandes que caminhamos para .
Agora iremos partir para a definição formal!
Passo 2
A definição precisa de limite diz que irá para em situações em que para todo , existe um tal que se , então
Em outras palavras, o que essa definição diz é que qualquer número negativo , deve existir um intervalinho próximo tal que o valor da função seja menor que . Como é arbitrário, os valores da função podem ser tomados tão pequenos quanto desejarmos e, assim, ela tenderá a .
Assim, o que devemos fazer é achar (possivelmente em função de ) tal que implica .
Passo 3
Seja e além de
Seja então um número real qualquer, podemos observar que por conta da propriedade dos logaritmos
Observe que a sugestão para dada acima. Então utilizando a definição e o valor de
Então, para qualquer , existe um (nesse caso ) tal que que implica que . Podemos confirmar o que pensamos visualizando o gráfico de novamente:
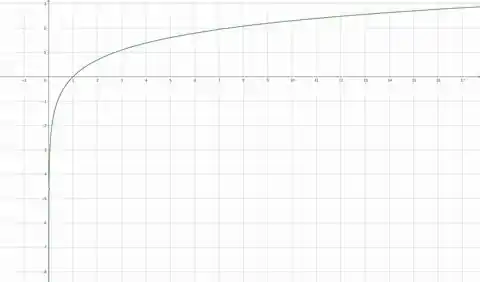
Resposta
Demonstração.