Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 19

Demonstre o volume de um tronco de cone circular reto

Passo 1

Dado o conte abaixo, fazendo um corte que passe perpendicularmente pela sua base até a sua ponta de cima, como na figura a seguir

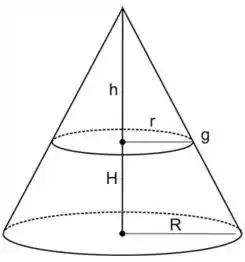
Aparece pra gente o seguinte triângulo retângulo

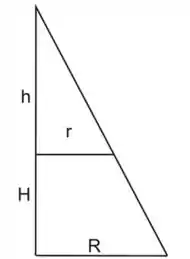
Se fizermos semelhança de triângulos, vamos ter o seguinte:

H + h h = R r

Passo 2

Trabalhando aquela expressãozinha para isolar h temos

H + h r = h R → H r + h r = h R → H r = h R - h r

h R - r = H r

h = H r R - r

O volume do tronco vai ser dado pelo seguinte

V T = V c o n e   m a i o r - V c o n e   m e n o r

V T = 1 3 π R 2 H + h - 1 3 π r 2 h = π 3 R 2 H + R 2 h - r 2 h

V T = π 3 R 2 H + R 2 - r 2 h

Substituindo o valor de h que achamos antes

V T = π 3 R 2 H + R 2 - r 2 H r R - r

V T = π H 3 R 2 + R 2 - r 2 r R - r

Usando a diferença de quadrados em R 2 - r 2 = R + r ( R - r ) , podemos simplificar um pouco mais, saca só:

V T = π H 3 R 2 + R + r R - r R - r r = π H 3 R 2 + R + r r

V T = π H 3 R 2 + R r + r 2

Resposta

V T = π H 3 R 2 + R r + r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = e - x ,y = 1 ,x = 2
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 + sec ⁡ x ,y = 3 ;
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x 2 ,x = y 2 ;e mt o
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 1e mt o r n od eB C
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = x - 2 4 ,8 x - y = 16 ; e mt o r n od oe i x