Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.7 - Ex. 34
Se denota a reação do corpo a algum estímulo de intensidade , a sensibilidade é definida como a taxa de variação da reação em relação a . Um exemplo acontece quando a luminosidade de uma fonte de luz é aumentada e o olho reage descrevendo a área da pupila. A fórmula experimental
tem sido usada para modelar a dependência de em quando é medido em milímetros quadrados em em uma unidade apropriada de luminosidade.
(a) Encontre a sensibilidade.
(b) Ilustre a parte (a) fazendo o gráfico de e como funções de . Comente sobre os valores de e em baixos níveis de luminosidade. Isso é o que você esperaria?
Passo 1
Opa, bora pra mais uma questão!
Temos uma formula que nos dá a área da pupila quando é exposto a luminosidade :
Onde é medido em e na unidade apropriada de luminosidade. Sabendo disso a gente deve calcular a sensibilidade que é a taxa de variação da reação em relação a .
Tem ideia de como fazemos isso?
Foi dito que é a variação de variação da reação em relação a . Ou seja, escrevendo isso de forma infinitesimal
Logo, se derivarmos em relação a vamos obter .
Por sua vez, se trata de uma fração de funções de , dessa forma, para calcular a derivada de podemos usar a regra do quociente.
Bora começar!
Passo 2
Primeiro vamos obter a função sensibilidade.
Pra isso a gente usa a regra do quociente:
Calculando as derivadas pela regra da potencia...
A partir daqui vamos simplificar nosso resultado...
Assim podemos simplificar
Portanto, a sensibilidade é dada pela função:
Tranquilo até aqui?
Passo 3
Para responder a letra (b) a gente vai plotar o gráfico de e em função de com a ajuda de uma ferramenta grafica:
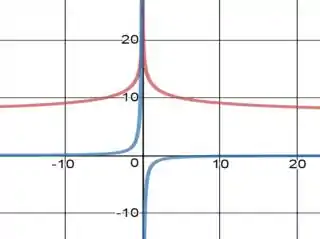
No gráfico acima, a aparece em vermelho e sua derivada em azul. Pelo gráfico quanto menor o módulo da intensidade do estímulo , mais a reação do corpo tende ao infinito e a sensibilidade tende ao infinito negativo à medida que a intensidade do estímulo tende a zero por valores maiores do que zero.
O que é esperado nesse caso, é que a descontinuidade da função permanece presente em sua derivada!
E aí! entendeu tudo? Responde Aí!
Resposta
(a) Sensibilidade é dada pela função .
(b) Quanto menor o módulo da intensidade do estímulo , mais a reação do corpo tende ao infinito e a sensibilidade tende ao infinito negativo à medida que a intensidade do estímulo tende a zero por valores maiores do que zero.