Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.8 - Ex. 8
O bismuto-210 rem uma meia vida de dias.
(a) Uma amostra tem originalmente uma massa de mg. Encontre uma fórmula para a massa remanescente depois de dias.
(b) Encontre a massa remanescente depois de dias.
(c) Quando a massa se reduzirá a mg?
(d) Esboce o gráfico da função massa.
Passo 1
Oiee bora láa
Esse enunciado descreve um problema de decaimento radioativo do isótopo bismuto-210, que tem uma meia-vida de 5,0 dias. A partir daí queremos encontrar uma fórmula para a massa remanescente em função de em dias para uma amostra de .
Com essa função em mãos, queremos encontrar a massa depois de dias, o tempo quando a massa cai para e esboçar o gráfico da função.
Parece complicado?
Fórmula para a massa remanescente depois de dias é dada pela formula do Teorema 2:
O tempo de meia-vida em questão é a cada dias, isso significa que a cada dias a massa ( com em dias) do elemento é reduzida pela metade. Se a massa inicial do elemento é mg.
Como a taxa de decaimento relativa é sempre constante, podemos relacionar massa do bismuto-210 com uma equação do Teorema 2.
veja só!
Passo 2
Neste caso, , mg, é o tempo em dias e é a taxa de decaimento relativo que pode ser calculada com os dados fornecidos.
Sabemos que quando dias a massa remanescente do bismuto-210 é a metade da massa inicial, ou seja, .
Logo, podemos aplicar na equação exponencial:
Para :
Como aparece multiplicando os dois lados, podemos simplifica-lo.
Agora temos que manipular essa equação para encontrar o valor de .
Isolando em um lado da igualdade:
Logo, a função para a massa remanescente depois de dias é:
Ou, simplificando:
Tranquilo até aqui?
Passo 3
Depois de obter a fórmula para a massa remanescente , podemos substituir dias na fórmula e calcular a massa remanescente.
A massa remanescente depois de dias corresponde a , então:
Resolvento essa equação...
(mg)
Logo, a massa após 30 dias é de 12,5 mg.
Bacana, não é?
Passo 4
Podemos resolver a equação mg para encontrar o tempo necessário para que a massa se reduza a 1 mg. Isso nos dará o tempo necessário para atingir esse valor específico.
A massa se reduzirá a mg quando mg, ou seja:
Vamos manipular essa igualdade para isolar em um lado.
Aplicando nos dois lados...
Pela propriedade do expoente no , temos:
Finalemente isolando em um lado da igualdade...
dias
Logo, a massa reduzirá a mg em aproximadamente dias.
Show?
Passo 5
Por fim, temos que representar a curva de ...
- Quando a curva corta o eixo .
- Perceba que a função está na forma , então pelo fato de estar negativo, a função é uma exponencial decrecente.
- Quando tende a , tende a , mas nunca de fato é .
- E como calculamos anteriormente, quando , .
A partir desses dados, podemos esboçar o gráfico de como:
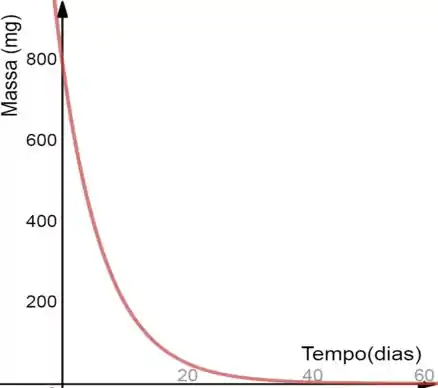
É isso! Entendeu tudo? Responde Aí!
Resposta
(a) .
(b) A massa após 30 dias é de 12,5 mg.
(c) A massa reduzirá a mg em aproximadamente dias.