Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.5 - Ex. 19
A densidade linear de uma barra de 8 m de comprimento é , onde x é medido em metros a partir da ponta da barra. Encontre a densidade média da barra.
Passo 1
Muito bem, antes de começar vamos lembrar de como se calcula o valor médio da função, ok?
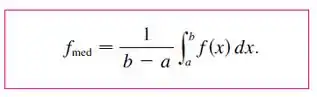
Tranquilo, não é? Dos seus 8 metros de comprimento, então vamos integrar a função de 0 até 8, tudo bem?
Só vamos substituir:
Tiramos as constantes:
Vamos ter que resolver por substituição:
Derivando:
Substituímos:
Resolvendo:
Substituindo u:
Aplicando o intervalo:
Resposta
Exercícios de Livros Relacionados
Encontre um valor positivo de k com o qual o valor médio de f x = 3 x acima do intervalo 0 ,k seja 6 .
Suponha que um tumor cresça a uma taxa de r t = k t gramas por semana, para alguma constante positiva k , onde t indica o número de semanas desde que ele surgiu. Quando, durante as semanas 27 a 52 , o
29- Um grande copo contendo 60 ml de suco de laranja está sendo reabastecido com mais suco. A figura Ex-29 mostra a taxa segundo a qual o suco está sendo vertido no copo em mililitros por segundo (ml/
Se um automóvel alcança uma média de 12k m por litro de gasolina, então também ocorre que, em média, esse automóvel gasta 1 / 12 de litro por km. Interprete essa afirmação usando o conceito de valor m
Considere a afirmação seguinte: O valor médio da taxa de variação de uma função em um intervalo é igual à taxa de variação média da função nesse intervalo. Escreva um parágrafo curto explicando por qu