Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.5 - Ex. 16

O gráfico da velocidade de um carro acelerado está mostrado a seguir.

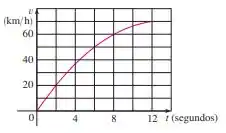
  1. Dê uma estimativa da velocidade média do veículo durante os primeiros 12 segundos.
  2. Em que instante a velocidade instantânea foi igual à velocidade média?

Passo 1

  1. v m é d i o = 1 12 - 0 ∫ 0 12 v ( t ) d t = 1 12 I .

    2. Usando a Regra do Ponto Médio para n = 3 e ∆ t = 12 - 0 3 = 4 para estimar I .

    I ≈ M 3 = 3 v 2 + v 6 + v 10 = 4 21 + 50 + 66 = 4 137 = 548

    Então, v m é d i o ≈ 1 12 548 = 45 2 3 k m / h .  

    Passo 2

  2. Estimando pelo gráfico, v t = 45 2 3 quando t = 5.2 s .

Resposta

  1. v m é d i o ≈ 45 2 3 k m h
  2. t = 5.2 s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. (Suponha que f e g denotem funções contínuas num intervalo [ a,b ] e que f m e g m denotem os respectivos valores médios de
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. (Suponha que f e g denotem funções contínuas num intervalo [ a,b ] e que f m e g m denotem os respectivos valores médios de
(a) A temperatura de uma barra de metal com 10m e t r o s de comprimento é de 15 ° C em uma ponta e de 30 ° C na outra. Supondo que a temperatura aumenta linearmente do extremomais frio para o mais qu
A água está fluindo a uma taxa constante de 1p é 3 / m i n é para encher um tanque cilíndrico com 3p é és de raio e 5p é s é de altura. Supondo que o tanque esteja vazio inicialmente, faça uma conject
(a) Suponha que a função velocidade de uma partícula movendo-se ao longo de um eixo coordenado seja v ( t ) = 3 t 3 + 2 . Encontre a velocidade média da partícula no intervalo detempo 1 ≤ t ≤ 4 por in