Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.8 - Ex. 29
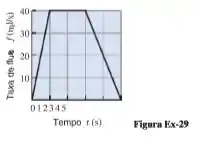
29- Um grande copo contendo 60 ml de suco de laranja está sendo reabastecido com mais suco. A figura Ex-29 mostra a taxa segundo a qual o suco está sendo vertido no copo em mililitros por segundo (ml/s). Mostre que a taxa de variação média do volume de suco no copo durante esses 5s é igual ao valor médio da taxa de fluxo do suco para dentro do copo.
Passo 1
Galerinhaaa, para descobrirmos a taxa de variação média do volume de suco no copo temos que descobrir a área da figura apresentada entre o gráfico da taxa de suco e o eixo do tempo. E olhem só.... Temos a figura de um trapézio, assim:
Mas esse é o valor total da quantidade de suco que foi transferida para dentro do copo. Para acharmos a média dessa variação é necessário dividirmos esse resultado pelo tempo total. Dessa forma,
Passo 2
Para descobrirmos o valor médio da taxa do suco para dentro do copo, temos primeiro que determinar a função descrita pelo gráfico. Temos, então:
Agora nós temos que usar a seguinte definição de valor médio:
Dessa forma,
Resolvendo as integrais:
Amiguíneos, o nosso que é a subtração dos nossos último e primeiro extremos de integração, respectivamente, pois esse é o intervalo que comporta a nossa função, Fechou ?!
Portanto, temos que que a taxa de variação média do volume de suco no copo durante esses 5s é igual ao valor médio da taxa de fluxo do suco para dentro do copo.
Resposta
Demonstração acima.