Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 56
A derivada à esquerda e à direita de em são definidas por
Se esses limites existirem. Então existe se, e somente se, essas derivadas unilaterais existirem e forem iguais.
- Encontre e para a função
- Esboce o gráfico de
- Onde é descontínua?
- Onde não é diferenciável?
Passo 1
Fala aí! como vai? 😬
Nesse problema temos que obter e da função
Além de esboçar o gráfico de e determinar onde é descontínua e não diferenciável.
Tem ideia de como fazemos isso? 😉
Primeiramente, lembremos que esses sinais de + e – no limite, indicam que estamos falando de limites laterais. O termo é limite quando se aproxima de 4 pela esquerda, ou seja, por valores menores que 4. Já é quanso e se aproxima pela direita.
Para obter e , usamos a definição de derivada:
Para obter o gráfico de , temos que plotar 3 curvas e pegar o trecho de cada uma delas referente aos seus intervalos, já que é definida por partes. E a partir do gráfico podemos dizer onde é descontinua e onde não é diferenciável.
Veja só! 😉
Passo 2
Aplicando a definição de derivada aos nossos limites laterais:
Então o primeiro passo é achar . Pra isso vamos substituir por em :
Como aqui o limite é pela esquerda, estamos falando de , então:
Já o valor da função quando , é dado por:
Voltando na definição de derivada:
E finalmente:
Agora vamos fazer o limite pela direita!
Passo 3
O limite pela direita é dado por:
No limite pela direita, , então vamos fazer:
E o valor de é o mesmo, então:
Igualando denominadores (no numerador):
Arrumando:
Simplificando e aplicando o limite...
Agora sim resolvendo o limite:
Tranquilo até aqui? 😁
Passo 4
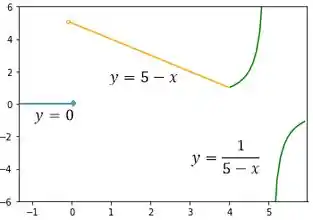
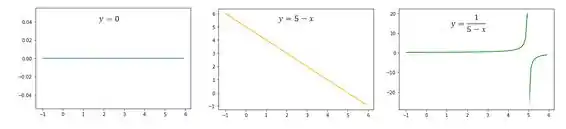
é uma função constante, uma reta horizontal.
é uma reta de inclinação negativa que cruza o eixo em 5
E a curva tem um ponto fora do seu domínio, o ponto que anula o denominador. Nesse ponto tempos uma assíntota vertical, ou seja, o gráfico explode pro infinito.
Esboçando essas partes em um único gráfico, temos
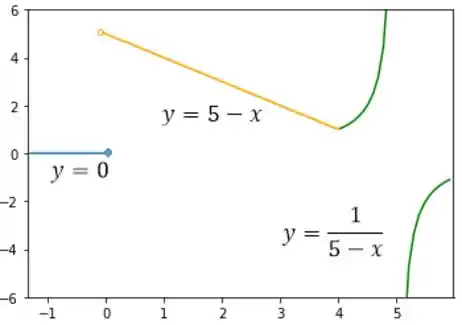
Bacana, não é? 😊
Passo 5
Pela expressão da função, podemos ver que é contínua nos intervalos e , porque funções constantes e polinomiais são continuas. E no caso de , só tem um ponto de descontinuidade que é que anula o denominador.
Então, precisamos analisar a continuidade nos pontos e .
i) Para :
Como os limites laterais são diferentes, é descontínua em .
ii) Para :
Como os limites laterais são iguais, é continua em .
iii) Para :
não está definida, logo e descontínua em .
Bacana, não é? 😬
Passo 6
Sabemos que uma função não é diferenciável nos pontos de descontinuidade, logo, não é diferenciável nos pontos e e em a função possui uma ponta, portanto nesse ponto tambem não é diferenciavel.
E aí! o que achou? Responde Aí! 😉
Resposta
a) e
b) e
c) e
