Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 39
O gráfico de é dado. Indique os números nos quais não é diferenciável.
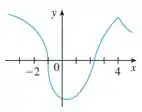
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente indicar os números nos quais a função , que é representada no gráfico, não é diferenciável.
Mas como uma função pode não ser diferenciável? Em geral, se o gráfico de uma função tiver uma “quina” ou uma “dobra”, então o gráfico de não terá tangente nesse ponto e não será diferenciável ali. Além disso, se tentarmos calcular os limites à esquerda e a à direita nesse ponto, esses limites serão diferentes.
Uma outra forma de uma função deixar de ter uma derivada em um ponto é se ela não for contínua nesse ponto, então não será diferenciável nesse ponto.
E uma terceira possibilidade surge quando a curva tem uma reta tangente vertical no ponto que queremos calcular a derivada. Nesse caso a função também não será diferenciável no ponto, porque a medida que se aproxima do ponto, a derivada da função tende pra infinito, ou seja, a reta tangente vai ficando cada vez mais íngreme.
Olha só a ilustração de exemplos desses três casos:
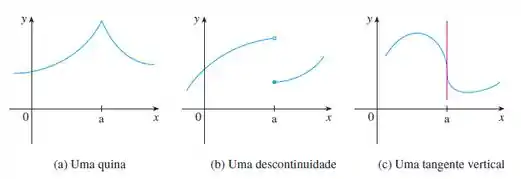
Então, são esses pontos que nós vamos procurar e tentar identificar no gráfico que o enunciado nos deu.
Vamos lá!
Passo 2
Vamos analisar o gráfico da nossa função:
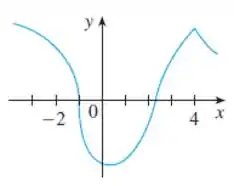
Olhando ali no ponto , a gente percebe que existe uma reta tangente vertical naquele ponto. Olha só como a curva tá retinha ali:
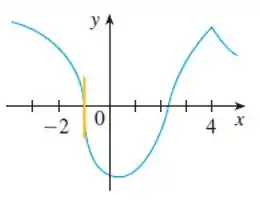
Isso recai em um dos casos que vimos no passo . Então, a função não é diferenciável em .
Além disso, repare que ali em temos um pico ou uma “dobra” na curva da função. Isso também indica que a função não é diferenciável em , conforme vimos no passo anterior.
Portanto, temos os seguintes pontos onde a função não é diferenciável:
Valeu, galera! Até a próxima! 😉