Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 37

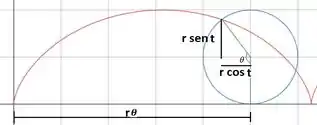
Derive as equações 1 para o caso π 2 < θ < π .

Passo 1

Para derivar as equações para o caso π 2 < θ < π , primeiro, vamos revisar as equações básicas do círculo. Em um círculo de raio r , as coordenadas ( x , y ) de um ponto na circunferência são dadas por:

x = r ⋅ c o s ( θ )

y = r ⋅ s e n ( θ )

A derivada de x em relação a θ :

d x d θ ​ = d ( r ⋅ c o s ( θ ) ) d θ = r ⋅ c o s ( θ )

d x d θ ​ = - s e n ( θ )

A derivada de y em relação a θ :

d y d θ ​ = d ( r ⋅ s e n ( θ ) ) d θ = r ⋅ s e n ( θ )

d y d θ ​ = c o s ( θ )

Passo 2

Agora basta substituir o intervalo nas derivadas.

Para θ = π 2

d x d θ ​ = - r . s e n   π 2   = - r

d y d θ ​ = r . c o s   π 2   = 0

Para θ = π

d x d θ ​ = - r . s e n   π   = 0

d y d θ ​ = r . c o s   π   = r

Resposta

O exercício pede para deduzirmos a equação paramétrica para a cicloide considerando π 2 < θ < π . Para isso, fazemos o seguinte desenho:

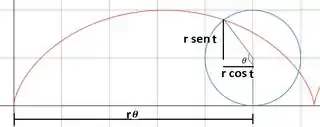
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Investigue a família de curvas dadas por r = 1 + c cos ⁡ θ , em que c é um número real. Como o formato muda conforme c varia?
Investigue a família de curvas dada por r = 1 + c o s n θ onde n é um inteiro positivo. Como muda o formato quando n aumenta? O que acontece quando n se torna maior? Explique a forma para o n maior co
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.70. r = t gθ c o t gθ (curva valentina)
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.71. r = 1 + cos 999 ⁡ θ (curva de PacMan)
67-72. Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira.72. r = s e n 2 4 θ + c o s ( 4 θ )