Investigue a família de curvas dada por onde é um inteiro positivo. Como muda o formato quando aumenta? O que acontece quando se torna maior? Explique a forma para o maior considerando o gráfico de como uma função de nas coordenadas cartesianas.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função polar:
Onde é um inteiro positivo.
Com uma calculadora gráfica, vamos plotar essa função para alguns valores de e analisar o que muda no formato do gráfico quando aumenta.
Por fim, ainda utilizando uma ferramenta matemática, vamos plotar essa função nas coordenadas cartesianas.
Passo 2
Vamos substiruir na função e observar os valres.
Para, temos:

Para , temos:
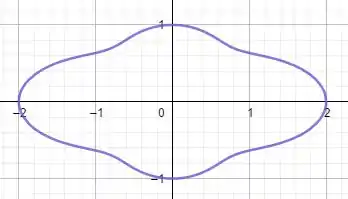
Para , temos:

Podemos ver que para pequeno a curva se parece com um amendoin, mas conforme aumenta seus polos são achatados até se parecer a uma circunferência com dois picos nas laterais.
Passo 3
Em coordenadas cartesianas, para , e , o gráfico fica:

Podemos perceber que, para pequeno, temos curvas cosenoidais que são bem suaves.
Mas quando fica muito grande as curvas começam a parecer cada vez mais com uma reta e ter um pico central, como podemos ver para , no centro temos aproximadamente uma função .
Isso acontece pois conforme aumenta se torna muito pequeno chegando cada vez mais próximo de zero, então .
Resposta
Demonstração