Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 75
Investigue a família de curvas dadas por , em que c é um número real. Como o formato muda conforme c varia?
Passo 1
Olá, meu amigo. Temos que investigar a família de curvas dadas pela equação:
Onde , é um valor real.
Então, como iremos investigar essa curva? Vamos colocar vários valores diferentes para e iremos ver como o gráfico da curva vai se comportando.
Eu irei fazer isso utilizando o GeoGebra, mas você pode utilizar o seu software favorito.
Passo 2
Os gráficos de são:
Para temos:
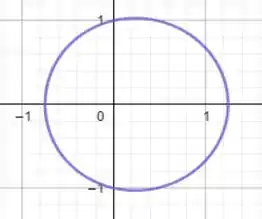
Para , temos:
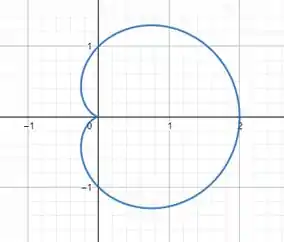
Para , temos:
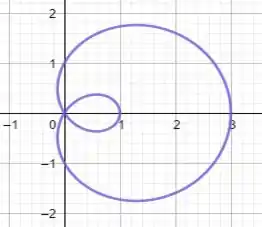
Para :
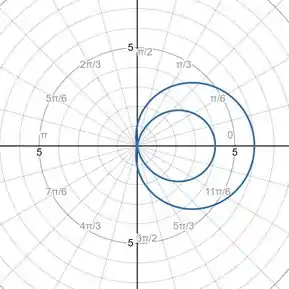
Passo 3
Quando é pequeno a figura é uma circunferência que não está centrada em zero, quando aumentamos o valor de o lado esquedo desta circunferência se achata para dentro formando outra circunferência no interior da primeira.
Percebemos também que o lado direito e as bordas superiores e inferiores também estão aumentando, sendo que o lado direito cresce com uma taxa maior que as bordas superiores e inferiores.
Resposta
Ver o desenvolvimento.