Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.1 - Ex. 8
Descreva e esboce a superfície no representada pela equação
Passo 1
A equação não possui restrições em , e as coordenadas e devem satisfazer a equação de um círculo de raio 3 com centro na origem. Sendo assim, a equação:
Consiste de todos os possíveis círculos, paralelos ao plano com raio 3 e cento na origem. O conjunto de todos esses círculos formará por sua vez um cilindro ao logo do eixo .
Passo 2
O gráfico do plano é mostrado a seguir.
Resposta
Exercícios de Livros Relacionados
12. Sabendo que o ângulo entre os vetores u → e v → é de 60 ° , determinar o ângulo formado pelos vetores:c) - u → e - v →
12. Sabendo que o ângulo entre os vetores u → e v → é de 60 ° , determinar o ângulo formado pelos vetores:b) - u → e 2 v →
13. Dado os vetores coplanares u → , v → e w → representados na Figura 1.36 determinar:c) O ângulo entre os vetores - 2 u → e - w → .
13. Dado os vetores coplanares u → , v → e w → representados na Figura 1.36 determinar:b) O ângulo entre os vetores - 3 v → e w → .
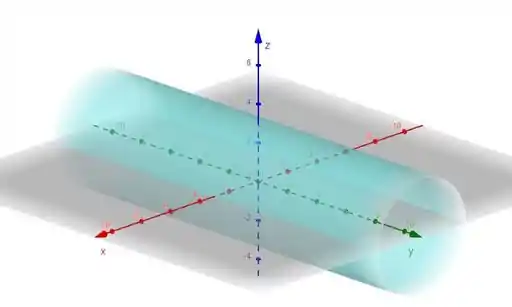
Demonstrar que o segmento de extremos nos pontos médios dos lados não paralelos de um trapézio é paralelo às bases e igual à sua semissoma.