Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 12b
12. Sabendo que o ângulo entre os vetores e é de , determinar o ângulo formado pelos vetores:
b) e
Passo 1
Então galera, para facilitar nossa visualização sobre o problema vamos esboçar os vetores e , assim como o ângulo formado entre eles, saca só:
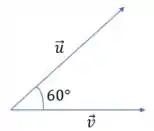
Essa é a situação descrita pelo enunciado, tudo bem? Show!
Passo 2
A questão quer que descubramos o ângulo formado pelos vetores e , mas como fazemos isso? Vamos analisar o que muda em cada um dos vetores, se liga:
No vetor só aparece um sinal de negativo na frente, mas no que isso implica? Isso implica que apenas o SENTIDO do vetor irá mudar. Já no vetor aparece um número multiplicando, e isso quer dizer que o nosso vetor foi dobrado! Esboçando nossa nova situação:
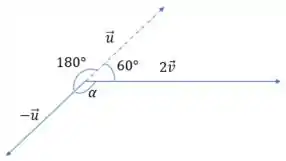
Queremos saber quanto vale esse ângulo agora! De acordo com o que aprendemos em trigonometria, uma volta completa vale , certo? Pelo nosso desenho temos o seguinte:
E esse é o ângulo entre nossos dois novos vetores, pessoal! 😉
Resposta
O ângulo é de .