Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.6 - Ex. 29
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
Passo 1
Temos os seguintes esboços da nossa função:
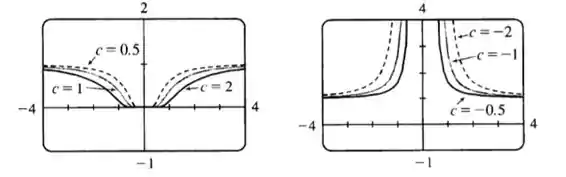
Com , nós temos o gráfico de . Para , notamos que há uma assíntota horizontal em , e o gráfico se espalha conforme aumenta. Na primeira janela, aparentemente há um ponto mínimo em , mas é indefinida, então não há máximo ou mínimo. Para , nós ainda temos uma assíntota horizontal em , mas o alcance é em vez de . Nós também temos uma assíntota vertical em .
Passo 2
Derivando :
e existe para todo diferente de , então não há valor mínimo ou máximo.
Então, se , os pontos de inflexão aumentam conforme aumenta, e se , não há ponto de inflexão. Para , há ponto de inflexão em . Note que a coordenada do ponto de inflexão é constante.
Resposta
Ei, a resposta está no passo a passo :)