Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.5 - Ex. 13
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Eaeee, belezinha??? Bom... A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.
Para iniciar a questão vamos relembrar um pouco da teoria:
Domínio: Conjunto de todos os valores de para os quais a função é definida.
Interseções com os Eixos:
- Eixo : Onde
- Eixo : Onde ou seja,
Simetria:
- Função Par:
- Função Ímpar:
Assíntotas:
- Assíntotas Verticais: Linhas verticais onde a função cresce sem limites.
- Assíntotas Horizontais: Linhas horizontais que a função se aproxima conforme
Derivadas e Comportamento da Função:
- Primeira Derivada Para determinar onde a função é crescente ou decrescente.
- Segunda Derivada Para determinar a concavidade e pontos de inflexão.
Os intervalos nos quais uma função é crescente (ou decrescente) correspondem aos intervalos nos quais sua derivada é positiva (ou negativa). Então, se quisermos encontrar os intervalos em que uma função é crescente ou decrescente, nós calculamos sua derivada e descobrimos onde ela é positiva ou negativa (o que é mais fácil!).
Concavidade e Pontos de Inflexão:
- Concavidade para cima:
- Concavidade para baixo:
- Pontos de Inflexão: Onde e muda de sinal.
Bora lá!! 😉
Passo 2
O domínio de uma função é o conjunto de todos os valores de entrada para os quais a função produz um resultado válido.
Sabendo disso, é importante observar as restrições que uma função pode ter.
O domínio da função é onde o denominador não é zero.
Desta forma, o domínio da função
Passo 3
A curva não tem raízes de modo que ela cruza o eixo pois, fazendo , temos:
Podemos observar a cima que haverá uma indeterminação.
Todavia, ela cruva o eixo : fazendo , obtemos que sua interseção com o eixo ocorre em:
Logo, temos o ponto .
Passo 4
Observe que a função é par, pois:
Portanto, a curva é simétrica em relação ao eixo .
Passo 5
Vamos agora procurar possíveis ass��ntotas. Para indo para :
Assim, tanto para como para , o eixo é assíntota horizontal da função.
Como tanto como não estão no domínio da função, temos que verificar se a curva tem assíntotas verticais nesse ponto.
Como a função é par, podemos verificar apenas para e caso ela tenha assíntota nesse ponto, terá em também!
Assim, as retas e são assíntotas verticais da curva.
Passo 6
Vamos estudar agora os intervalos de crescimento e decrescimento da função. Calculando a primeira derivada:
Como , o sinal da derivada será
Assim, o ponto é ponto de máximo local.
Passo 7
Por fim, vamos analisar a concavidade da curva. Fazendo a segunda derivada:
Como , apenas o denominador vai importar para o sinal de :
Com base nessas informações, temos o seguinte esboço:
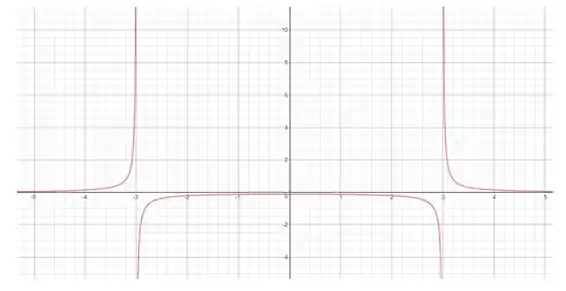
Entendeu direitinho?? Responde aee 😉
Resposta
O esboço da curva:
