Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.2 - Ex. 34
Mostre que a área da superfície de uma zona de uma esfera entre dois planos paralelos é , em que é o diâmetro da esfera e , a distância entre os planos. (Observe que depende apenas da distância entre os planos e não de sua localização, desde que ambos os planos interceptem a esfera.)
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa querida atividade.
Precisamos lembrar da equação de uma esfera, beleza?! A equação da esfera é da forma
Sabemos que , então
Vamos agora, dizer que os planos interceptam a esfera nas retas e .
Podemos fazer um gráfico dos interceptos da esfera no eixo (transformar o desenho para 2D)
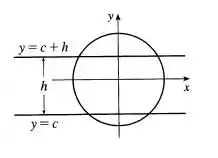
Dessa forma, podemos calcular a área da superfície da uma zona da esfera entre os dois planos como a rotação dessa curva em torno do eixo .
Passo 2
Em 2D, a esfera vira um círculo, e o círculo tem como equação
Você se lembra de como calculamos a área de uma superfície gerada pela revolução de uma curva em torno do eixo ? Não?! Então vamos relembrar. Temos que a área é dada por
Então, na equação do círculo, vamos calcular a derivada em relação a
Então, a área é
Retirando a constante da integral:
Colocando para dentro da raiz:
Simplificando:
Sabendo que :
Realizando a integração