Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 33
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
Passo 1
Oieee, tudo bem?
Bora resolver comigo?
Para entender como o gráfico de
Varia conforme muda, vamos examinar o comportamento da função e identificar os pontos de máximo, mínimo e inflexão.
Limites quando tende a
Assim como antes, podemos calcular os limites quando tende a
Para esta função, quando tende a tende a zero, independentemente do valor de
Isso ocorre porque o termo domina o denominador quando se torna grande o suficiente, tornando muito maior do que
Comportamento dos pontos de máximo, mínimo e inflexão quando varia:
- Pontos Críticos: Para encontrar os pontos críticos, derivamos em relação a e igualamos a zero:
Simplificando e resolvendo, obtemos os pontos críticos.
Passo 2
No entanto, para igualar a zero, o numerador deve ser zero:
Isso nos dá dois pontos críticos:
Estes serão os pontos onde a função tem potenciais máximos ou mínimos.
Passo 3
- Pontos de Máximo e Mínimo: Para determinar se esses pontos são máximos ou mínimos, podemos usar o teste da segunda derivada.
A segunda derivada é:
Avaliando em , obtemos:
Se então
Indicando que esses pontos são mínimos.
Se então
Indicando que são máximos.
Passo 4
- Pontos de Inflexão: Para encontrar os pontos de inflexão, precisamos verificar onde a concavidade muda.
Como a segunda derivada é uma função par, não haverá pontos de inflexão.
Podemos traçar vários membros da família de curvas para diferentes valores de para visualizar melhor como a forma da curva muda. Podemos traçar para
Isso nos ajudará a entender como a inclinação da curva muda com
Passo 5
Esboço do gráfico:
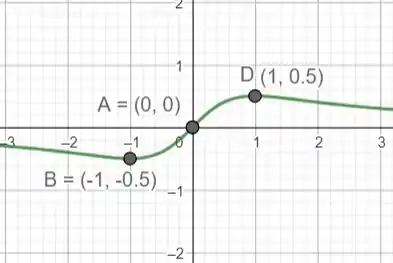
Com base nessas observações, podemos esperar que o gráfico da função tenha uma série de comportamentos distintos, incluindo assíntotas verticais, pontos de máximo e mínimo, e diferentes padrões de concavidade, dependendo do valor de como mostra o gráfico abaixo.
Quando a função tem uma concavidade voltada para cima, enquanto a função tem uma concavidade voltada para baixo
Resposta
Vide a explicação.