Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 23
Faça o gráfico da função usando quantas visualizações retangulares você precisar para descrever a verdadeira natureza da função.
Passo 1
E aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é plotar o gráfico de usando uma visualização retangular que descreva a natureza real dessa função.
Parece complicado?
Para resolver esse problema temos que usar uma ferramenta gráfica para plotar o gráfico da função e a partir daí vamos analisar qual é o melhor intervalo que podemos plotar essa função para podermos ter uma real noção do seu comportamento.
Saca só!
Passo 2
Primeiro podemos perceber que e que é uma função par pois aparece sempre com expoente par, logo seu gráfico possui simetria em torno do eixo .
Para está função fizemos duas visualizações retangulares:
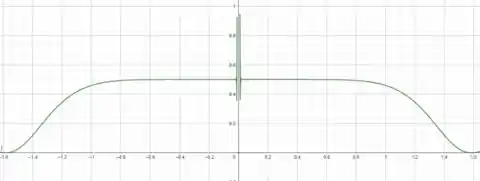
Nessa primeira podemos observar um comportamento um tanto quanto instável próximo de .
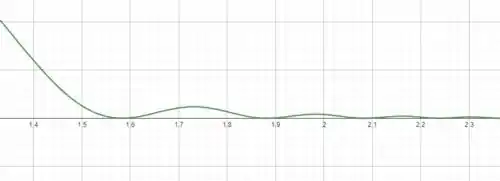
E conforme cresce, tende a com uma pequena oscilação que vai diminuindo.
E aí! o que achou? Responde Aí!
Resposta
O primeiro gráfico mostra que se estabiliza para para . Também mostra que decai para o eixo . O gráfico mostra algumas oscilações graves perto da origem mas elas não existe (Leia sobre Mentiras que a minha calculadora e computador me contaram).
E o segundo gráfico indica que a medida que aumenta, tem amplitudes progressivamente menores.