Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 80

Uma função cúbica é um polinômio de grau três; isto é, tem a forma f x = a x 3 + b x 2 + c x + d , em que a ≠ 0 .

  1. Mostre que uma função cúbica pode ter dois, ou nenhum número(s) crítico(s). Dê exemplos e esboços que ilustrem essas três possibilidades.
  2. Quantos valores extremos locais uma função cúbica pode ter?

Passo 1

Faaaala falaaaa. Nessa questão temos uma função cúbica genérica:

f x = a x 3 + b x 2 + c x + d

Onde a ≠ 0 .

E temos que provar na letra a) que ela pode ter dois ou nenhum número crítico.

Sendo que o número crítico é o ponto onde a derivada da função é igual a zero.

E então dar exemplo e esboço.

Por fim, na letra b), vamos mostrar quantos valores extremos locais a função cúbica pode ter.Basicamente, um ponto crítico pode ser um valor extremo local (ele pode ser máximo local ou mínimo local), portanto, o número máximo de pontos críticos que encontrarmos vai ser o número máximo de extremos locais que a função pode ter.

Passo 2

Uma função cúbica genérica é:

f x = a x 3 + b x 2 + c x + d

Assim sendo, nossa derivada será

f ' x = 3 a x 2 + 2 b x + c

Que é uma função de segundo grau

Agora igualando a zero

3 a x 2 + 2 b x + c = 0

Que é uma raíz quadrática, e consequentemente, tem 2 ,   1 ou 0 raízes reais.

x = - b ± b 2 - 4 a c 2 a

Assim f ( x ) tem 0 ,   1 ou 2 números críticos.

Passo 3

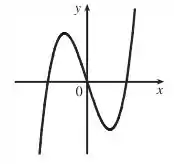
Exemplo 1 com dois números críticos:

f x = x 3 - 3 x

f ' x = 3 x 2 - 3

f ' x = 0

3 x 2 = 3

x = ± 1

1 e - 1 são números críticos.

Gráfico:

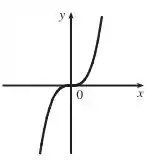
Exemplo 2 com 1 número crítico:

f x = x 3

f ' x = 3 x ²

f ' x = 0

x = 0

0 é o número crítico.

Gráfico:

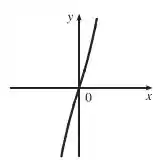
Exemplo três com nenhum número crítico:

f x = x 3 + 3 x

f ' x = 3 x 2 + 3

f ' x = 0

3 x 2 = - 3

Como não há raiz de número negativo, não há número crítico.

Gráfico:

Passo 4

Como há no máximo dois números críticos, pode haver no máximo dois valores extremos locais e como no exemplo 1, isso pode ocorrer. Como no exemplo 3, pode ser que não haja nenhum valor extremo. No entanto, se há apenas um número crítico, logo, não há valor de extremo local.

Resposta

a)

Como a derivada resulta em uma função de segundo grau, ela possui até 2 raízes e portanto a função possui até 2 números críticos.

b)

Como a função possui até 2 números críticos ela possui até 2 pontos extremos locais (máximos e/ou mínimos).

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que f seja derivável até a 2ª ordem em R e tal que para todo x . x f ' ' x + f ' x = 2 Prove que, se x 0 for ponto de máximo local, então x 00 .Prove que, se x 0 for ponto de mínimo local, ent
Seja f derivável em R e seja g dada por g x = f x x , x ≠ 0 . Suponha que p é ponto de máximo local de g .Prove que p f ' p - f p = 0 .Prove que a reta tangente ao gráfico de f no ponto de abscissa p
Suponha que f seja derivável até a 2ª ordem em R e tal que para todo x . f ' ' x + x f ' x = 1 Prove que f não admite ponto de máximo local.Prove que, se f admitir um ponto crítico x 0 , então x 0 ser
Identifique os valores extremos locais das funções nos domínios dados informe onde eles ocorremQual dos valores extremos, se houver, é absolutoFundamente suas conclusões como uma calculadora ou progra
Identifique os valores extremos locais das funções nos domínios dados informe onde eles ocorremQual dos valores extremos, se houver, é absolutoFundamente suas conclusões como uma calculadora ou progra