Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 56
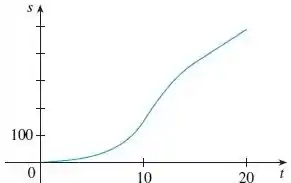
- É mostrado o gráfico da função posição de um veículo, onde é medido em metros e em segundos. Use-o para traçar a velocidade e a aceleração do veículo. Qual é a aceleração em segundos?
- Use a curva da aceleração da parte (a) para estimar o jerk em segundos. Qual a unidade do jerk?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu o gráfico da posição versus o tempo , do movimento de um veículo:
Queremos traçar a velocidade e a aceleração desse veículo, usando o gráfico.
Além disso, vamos precisar determinar a aceleração do veículo no tempo e usar a curva para estimar o jerk (que nada mais é do que uma quantidade física que representa a taxa de variação da aceleração) nesse mesmo instante.
Mas vamos por partes...
Primeiro vamos ter que traçar o gráfico da velocidade e da aceleração, baseados apenas no gráfico da posição.
Pra isso, temos que lembrar que a velocidade é definida como a taxa de variação da posição em função do tempo , ou seja:
E que a aceleração é definida como a taxa de variação da velocidade em função do tempo :
Então, vamos observar nosso gráfico e estimar como essas variações ocorrem.
Depois disso, vamos usar a curva da aceleração, que obtivemos no primeiro item, e estimar o jerk em .
Vamos lá!
Passo 2
Vamos dar uma olhadinha na nossa curva:
Repare que a curva está aumentando muito lentamente no intervalo e há um rápido aumento no próximo intervalo
Isso significa que a taxa de variação da função é muito baixa no intervalo e muito alta no intervalo .
Sendo assim, podemos estimar uma velocidade máxima em . Então, o gráfico da velocidade começa crescente, tem um pico em e depois passa a ser decrescente.
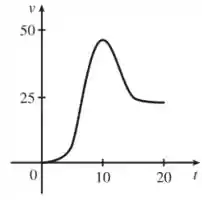
Passo 3
Agora repare que no instante , onde a velocidade é máxima, a reta tangente nesse ponto é horizontal.
Isso significa que a taxa de variação da velocidade nesse ponto é nula, ou seja, temos uma aceleração igual a zero nesse instante:
Considerando que a curva corta o eixo nesse instante e os intervalos de crescimento e decrescimento que observamos, vamos ter a curva da aceleração versus tempo:
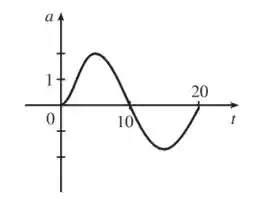
Passo 4
Agora desenhando uma linha tangente em no gráfico de , vemos que parece decrescer a por um período de segundos.
Logo, em , o jerk é aproximadamente:
Prontinho, galera! Até a próxima! 😉