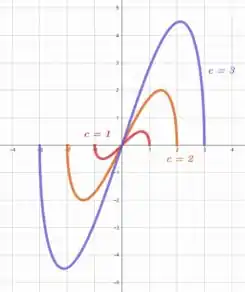
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.

A primeira coisa que podemos perceber é que como tem um expoente par, vamos ter uma simetria de comportamento da função , então vamos considerar apenas . Com , o gráfico de é apenas o ponto .

Além disso, temos uma simetria ímpar

O domínio de é encontrado resolvendo , o que nos dá .

Vamos ver como se comporta para , e .

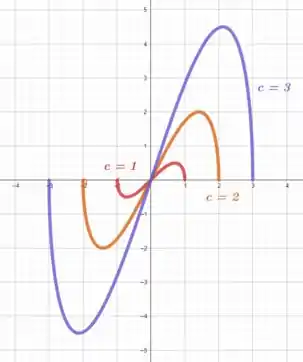
Tranquilo até aqui?

Agora vamos analisar as derivadas...

Derivando pela regra da cadeia e do produto...

A partir de , podemos determinar os intervalos de inclinação... para temos que tem inclinação positiva, ou seja

Assim, temos que cresce em e decresce em e em .

A função decresce até , e começa a crescer, então aí temos um ponto de mínimo, depois cresce até e torna a decrescer, nos dando um ponto de máximo, assim, temos os seguintes valores:

E pela simetria ímpar, temos

Tranquilo até aqui?

Vamos calcular a segunda derivada de pela regra do quociente.

Assim, quando , ou , mas apenas está no domínio de .

Temos para , e para , portanto, é côncava para baixo em e côncava para cima em

Há um ponto de inflexão em pois .

Com isso, sabemos que conforme o módulo de aumenta, os valores máximos e mínimos aumentam em magnitude, e o valor de não afeta a concavidade de .

É isso! O que achou? Responde Aí!