Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 38
Investigue a família de curvas dadas pela equação . Comece determinando o valor de transição de em que o número de pontos de inflexão muda. Faça então o gráfico de vários membros da família para ver quais formas são possíveis. Existe outro valor de transição de no qual a quantidade de números críticos muda. Tente descobrir isso graficamente. Demonstre então o que você descobriu.
Passo 1
Para , não há ponto de inflexão; a curva é côncava para cima em toda a parte. Se aumenta, a curva simplesmente se torna mais íngreme, e ainda não há pontos de inflexão. Se começa em e decresce, uma leve protuberância para cima aparece perto de , então ali há dois pontos de inflexão para qualquer . Isso pode ser visto algebricamente calculando a segunda derivada:
Então, quando .
Para , há pontos de inflexão quando .
Passo 2
Quando , o gráfico tem um número crítico, no mínimo absoluto em algum lugar em torno de . Conforme cresce, o número de pontos críticos não muda. Se ao invés disso decrescer a partir de , nós vemos que o gráfico eventualmente aparece outro mínimo local, à direita da origem, em algum lugar entre e . Consequentemente, há também um máximo perto de .
Passo 3
Depois de um pouco de experimentação, nós encontramos que em , parece haver dois pontos críticos, o mínimo absoluto em , e a tangente horizontal com nenhum valor extremo em .
Para qualquer menor que esse, haverá três pontos críticos, como mostrado no gráfico com , e com :
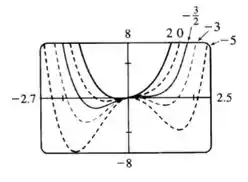
Para provar isso algebricamente, nós calculamos . Agora, se nós substituirmos nosso valor de , a fórmula para se torna . Isso tem uma raiz dupla em , indicando que a função tem dois pontos críticos: e . Assim como se nós tivéssemos adivinhado do gráfico.
Resposta
Ei, a resposta está no passo a passo :)