Desenha o gráfico de e de seu plano tangente no ponto dado. (Utilize um sistema algébrico computacional tanto para computar as derivadas parciais quanto para traçar os gráficos da função e de seu plano tangente). Em seguida faça uma ampliação até que sua superfície e o plano tangente se tornem indistinguíveis.
Passo 1
Show de bola, galera. A gente tem aqui uma questão gráfica de planos tangentes.
Basicamente precisamos plotar essa função e esse plano seguindo as especificações da questão? Mas como fazemos isso, e onde?
Você pode plotar esses gráficos em qualquer software! Idealmente se usaria o MATLAB, mas também temos softwares gratuitos como o GeoGebra!
Tá, mas e como eu encontro esse plano?
Para uma função com derivadas parciais contínuas, podemos descrever a equação do plano tangente no ponto como:
Assim, só precisamos definir todos os termos dessa equação e jogar no software!
Passo 2
A função nos diz para usar o ponto
Então vamos começar definindo o valor de !
Substituindo os valores de e na função, encontramos
De forma que
Passo 3
Agora precisamos encontrar as derivadas parciais para substituir na equação do plano
Utilizando o próprio software de sua escolha, chegamos nas seguintes derivadas parciais
Dessa forma, substituindo na fórmula do plano tangente, teremos o seguinte:
Aplicando o ponto nós encontramos:
Passo 4
Utilizando agora o Geogebra para plotar a função e o plano tangente nós teremos:
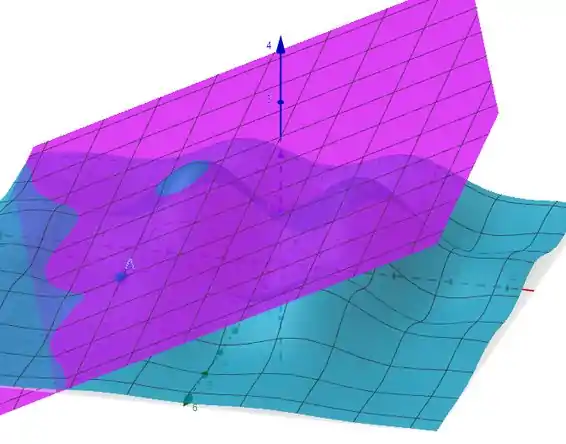
Agora se ampliarmos:
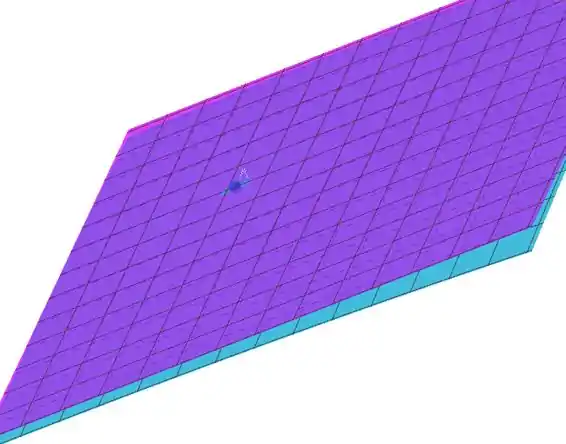
Onde o ponto é o ponto .
Resposta
Gráficos do passo 2.