Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 3
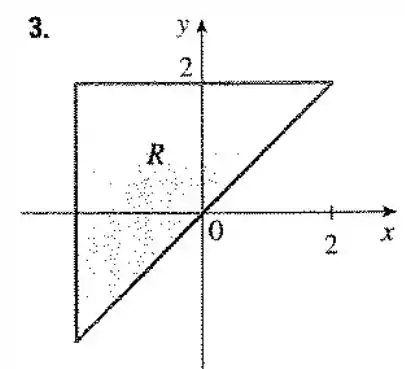
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma arbitrária qualquer contínua em .
3.
Passo 1
Fala ai, vamos entender o que a questão está pedindo, beleza???
Ele quer que a gente monte a integral, porém ele não nos fornece os intervalos e nem a função.
Porém a ideia dessa questão é que a gente seja capaz de fazer isso a partir de uma região, no caso no exercício, o triângulo .
Assim a primeira coisa que vamos fazer é escolher qual tipo de coordenada vamos usar, ok?
Por ser uma figura formada por linhas retas então é melhor utilizarmos coordenadas cartesianas. E podemos utilizar a integral por linhas verticais (tipo 1)
Então vamos precisar encontrar o domínio , ou seja :
Vamos nessa!!!!!!
Passo 2
Para a gente descobrir os limites temos que nos fazer a seguinte pergunta.
Qual maior e o menor valor que o pode adotar?
Vamos olhar a figura:
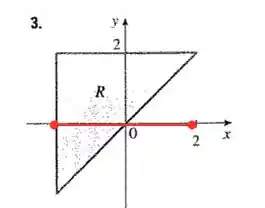
Podemos ver que o maior valor de será o porém como vamos descobrir o menor valor se ele não deu esse ponto ????
Ahhh, aqui vai o bizu.
Podemos ver que temos uma reta do tipo , porque um dos pontos pertencentes será , mas com essa informação ainda não podemos descobrir o menor valor para .
Porém se desenharmos uma reta anti simétrica , poderemos descobrir o ponto Saca só:
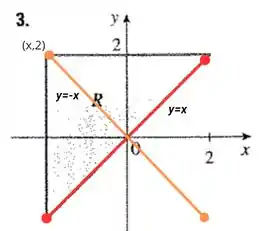
Para descobrir quem vai ser o ponto , vamos substituir na fórmula :
Oba, então descobrimos que o menor valor de será e o maior será . Então seus limites serão
Passo 3
Agora que sabemos o intervalo de vamos definir os intervalos de .
A gente sabe que o varia de acordo com o , lembra??
então qualquer valor de que a gente coloque no vai fazer o variar. Mas a gente também sabe que essa reta acaba no ponto , logo o maior valor que o terá , será .
Dessa forma:
Passo 4
Agora sabendo dos limites de integração podemos montar a nossa integral:
onde :
substituindo :
Resposta
Coordenadas cartesianas.