Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.4 - Ex. 9
Desenhe o gráfico de e de seu plano tangente no ponto dado. (Utilize um sistema de computação algébrica tanto para calcular as derivadas parciais quanto para traçar os gráficos da função e de seu plano tangente.) Em seguida, dê zoom até que a superfície e o plano tangente perto do ponto se tornem indistinguíveis.
Passo 1
Show de bola, galera. Antes de sairmos plotando os gráficos, precisamos calcular primeiro a equação do plano tangente no dado ponto. 
Primeiro precisaremos calcular as derivadas parciais e no ponto :
Desta forma, temos a seguinte equação para o plano tangente:
Passo 2
Seguindo a lógica do enunciado, chegamos nos seguintes gráficos:
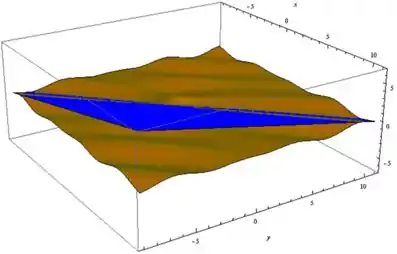
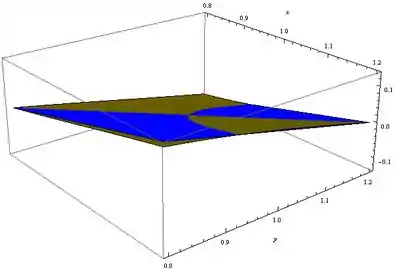
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Mostre que as pirâmides cortadas do primeiro octante por qualquer plano tangente à superfície x y z = 1 em pontos do primeiro octante têm todas o mesmo volume.
57 - Mostre que todo plano que é tangente ao cone z 2 = x 2 + y 2 passa pela origem.
Mostre que a equação do plano tangente a elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 pode ser escrita como x x 0 a 2 + y y 0 b 2 + z z 0 c 2 = 1
Encontre as equações paramétricas das retas tangentes a curva da intersecção do paraboloide z = x 2 + y 2 e da elipsoide 4 x 2 + y 2 + z 2 = 9 no ponto - 1,1 , 2 .
Existem pontos no hiperboloide x 2 - y 2 - z 2 = 1 nos quais o plano tangente é paralelo ao plano z = x + y ?