Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 13e
Desenhar algumas curvas de nível e esboçar o gráfico:
(e)
Passo 1
Pessoal, curvas de nível são sempre subconjuntos do domínio da função e, portanto, são traçados no plano . Cada curva de nível é a projeção da interseção do gráfico da função com o plano horizontal . Logo, para obtermos uma visualização de , podemos traçar várias curvas de nível e imaginamos cada uma dessas curvas deslocadas para a altura .
Assim, queremos traçar as curvas de nível da função . Traçando as curvas de nível, temos a seguinte imagem:
O gráfico da função é:
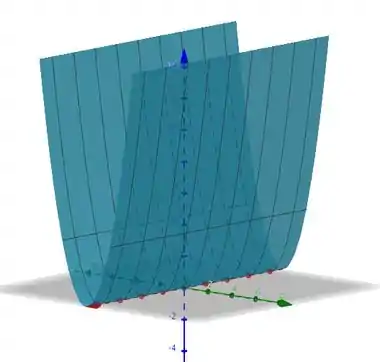
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Seja S a superficie definida por z = 2 + x 2 + y 2 .Faça o esboço de S .
Seja S a superficie definida por z = 2 + x 2 + y 2 .Identifique a interseção de S com o plano z = k , quando k2 , k = 2 e k2 .
Seja S a superficie definida por z = 2 + x 2 + y 2 .Identifique as interseções de S com os planos x z e y z .
Dada a função f x , y = 1 x 2 + y 2 , pede-se:A equação e o esboço da curva de nivel que contém o ponto ( 0,2 ) .
Dada a função f x , y = 1 x 2 + y 2 , pede-se:As equações das curvas de nível z = 1 4 , z = 4 e z = 9 .