Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 4b
Dada a função , pede-se:
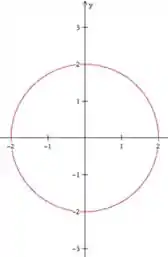
A equação e o esboço da curva de nivel que contém o ponto .
Passo 1
Bom galera, pra isso a gente começa colocando na nossa função os valores e , vamos lá:
Passo 2
Belezinha, agora substituímos esse valor de na função para encontrarmos a equação da curva de nível:
Passo 3
Por fim, fazemos o esboço, que é:
Resposta
Exercícios de Livros Relacionados
Identificar as afirmações verdadeiras:b) Os pontos P ( 0 ,4 ) e Q ( 2 ,2 ) pertencem à fronteira do conjunto B = { x , y ∈ R 2 | y4 - x 2 } .
Identificar as afirmações verdadeiras:e) Toda bola aberta é um conjunto aberto.
Representar graficamente os seguintes subconjuntos de R 2 . Identificar os conjuntos abertos. { x , y ∈ R 2 | x + y ≤ 1 }
Representar graficamente os seguintes subconjuntos de R 2 . Identificar os conjuntos abertos. x , y ∈ R 2 x ≥ 2 y - 3 }
Representar graficamente os seguintes subconjuntos de R 2 . Identificar os conjuntos abertos. { x , y ∈ R 2 | x 2 - 4 x + y 20 }