Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1a
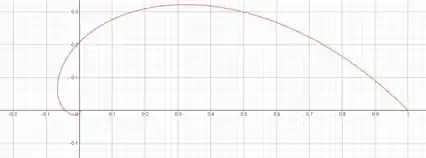
Desenhe a curva dada (coordenadas polares ).
Passo 1
Primeira coisa na hora de desenhar um gráfico é retirar o máximo de informação possível da função que descreve a curva.
Pro nosso caso podemos ver que a função é decrescente, já que conforme a variável cresce, a função diminui, veja:
Para já para , como sabemos que então:
Essa ideia é importante, por que a partir dela sabemos que o raio só vai diminuir conforme aumenta o valor de .
Passo 2
A segunda coisa é montar uma tabela com os valores de e de .
Para isso, vamos aproveitar valores bem conhecidos, como os de ângulos essenciais, como o ângulo de 30° que em radianos é, ou 45° que em radianos é e desses ângulos podemos pegar seu múltiplos para ter uma noção legal.
Mas por que esse ângulos?
Por que o “plano cartesiano” no sistema de coordenadas polares depende de um semi-eixo Ox e um ângulo, daí dividimos em intervalos grandes com esses múltiplos em radianos para podemos ter vários pontos interessantes e construirmos o gráfico. Entre esses pontos, temos uma noção de como eles se comportam e por isso conseguimos ter um gráfico com comportamento aproximado.
Vamos pra tabela:
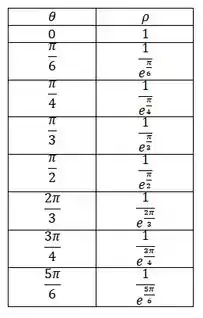
Passo 3
O desenho vai ficar mais ou menos assim:
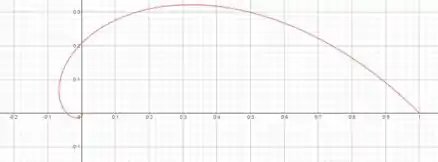
Repare que com a função é então , ou seja, o vai ser decrescente mas nunca vai chegar a 0.
Resposta
