Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 1g
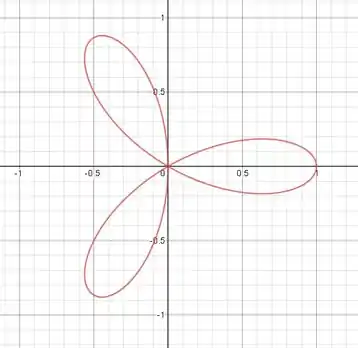
Desenhe a curva dada (coordenadas polares ).
Passo 1
Para esse caso devemos pegar valores que sejam compatíveis com os que já sabemos localizar, porém graças a esse pode ser difícil de calcular com os valores tradicionais, então vamos pegar valores 3 vezes menores, pra que quando nós jogarmos os valores, tenhamos valores de conhecidos.
Outra coisa importante é sabermos que , já que veremos que para o caso dado não iremos ultrapassar esse valores
Passo 2
A tabela fica assim: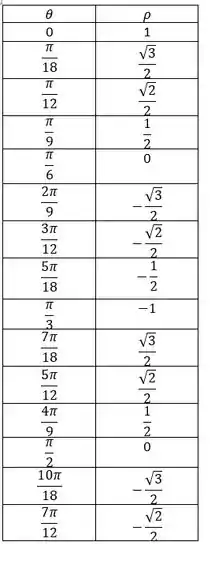
Agora temos que analisar com calma, por que o 0 aparece 3 vezes, o que quer dizer que ele passa por lá 3 vezes.
Mas porque eu escolhi parar nesse ponto ? Por que 0 e são dois extremos, ou seja, se um tem e o outro , então eles estão no memso lugar, o que significa que eles se encontraram.
Passo 3
Se você fizer o desenhos dos pontos e liga-los, vai ficar com um desenho assim:
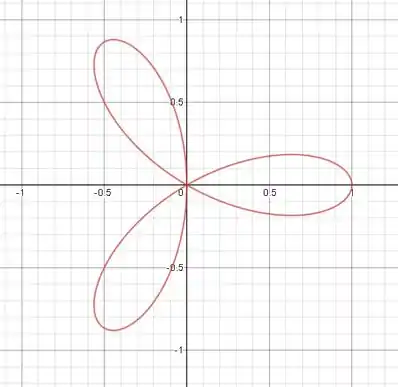
É uma rosácea de 3 folhas
Resposta
