Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.2 - Ex. 4
Desenhe o gráfico da função definida em [0, 8] que tenha e e que a função não satisfaça à conclusão do teorema do valor médio em [0, 8].
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que nosso probleminha está falando. Bom, ele nos pede para desenhar o gráfico da função com aquelas especificações que não obedeça ao teorema do valor médio.
Para desenhar o gráfico de uma função que satisfaça as condições fornecidas e não satisfaça a conclusão do Teorema do Valor Médio no intervalo podemos construir uma função que seja descontínua ou com uma descontinuidade em algum ponto dentro do intervalo.
Uma forma de fazer isso é criar uma função composta que consiste em duas partes: uma função linear que representa uma inclinação constante de e outra função linear que representa uma inclinação diferente de
Passo 2
Vamos definir a função dessa maneira:
- Para usaremos uma função linear que conecta os pontos onde é um valor que pode variar.
- Para usaremos outra função linear que conecta os pontos
Dessa forma, a função será descontínua em o que viola a condição para o Teorema do Valor Médio.
Vamos desenhar o gráfico dessa função. Vou usar como exemplo, mas você pode ajustar esse valor conforme desejar:
- Para
- Para
Passo 3
Como o enunciado pediu para que a conclusão não fosse respeitada, então não podemos ter um ponto com que sua tangente seja paralela ao eixo que liga os valores dos extremos.
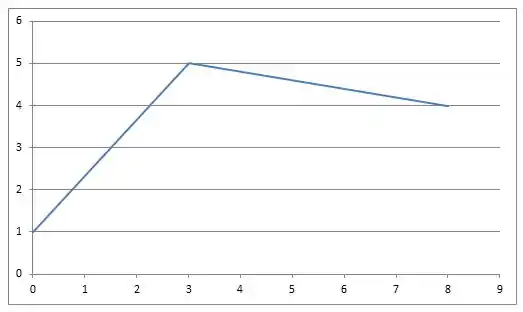
Neste gráfico, a função é uma linha reta de e então de . Essa função não satisfaz a conclusão do Teorema do Valor Médio no intervalo devido à descontinuidade em
Resposta
Vide a explicação.