Encontre o gráfico da função f contínua no intervalo [1, 5] com as seguintes propriedades.
Máximo absoluto em 4, mínimo absoluto em 5, máximo local em 2 e mínimo local em 3.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que nosso probleminha está falando!
. Bom, ele nos pede para montar um gráfico de uma função contínua no intervalo e com os seguintes pontos de máximo e mínimo:
-Máximo absoluto: ;
-Mínimo absoluto: ;
-Máximo local: ;
-Mínimo local: ;
Aqui a gente tem um quebra cabeça! Não existe só uma resposta certa mas é importante que o nosso gráfico contemple as características acima. Como temos uma função contínua com máximos e mínimos, então ela pode ser uma parábola!
esses pontos de máximo e mínimo de uma função contínua, ou seja, com pedaços como se fizessem uma parábola.
Para traçar o gráfico da função com as propriedades fornecidas, precisamos seguir estas etapas:
-1. Identificar os pontos críticos e extremos (Isso o enunciado já fez por a gente!);.
-2. Determinar a concavidade da função em torno dos pontos críticos. Os pontos críticos são os máximos e mínimos dados no enunciado. Um ponto mínimo é um local onde a concavidade é pra baixo e o ponto máximo teremos uma concavidade pra cima;
3.- Desenhar o gráfico da função garantindo que atenda aos critérios especificados.
Passo 2
Vamos começar com os passos:Como o enunciado já nos deu os pontos críticos e os pontos extremos, que é o início e final do intervalo, e , vamos partir direto pra análise de concavidade:
Vamos identificar os pontos críticos e extremos:
- Máximo absoluto em e mínimo absoluto em
- Máximo local em e mínimo local em
Vamos determinar a concavidade:
- O máximo absoluto em indica que a função deve ser crescente antes desse ponto e decrescente depois;estar em declive antes e depois desse ponto.
- O mínimo absoluto em indica que a função deve ser crescente após esse ponto;.
- O máximo local em indica que a função deve ser decrescente antes desse ponto e crescente depois;.
- O mínimo local em indica que a função deve ser crescente antes desse ponto e decrescente depois.
Agora vamos resumir como o nosso gráfico deve ser:
Para finalizar iremos desenhar o gráfico:
- Com base nas informações acima, podemos traçar uma função que comece de um valor mais alto em atinge um máximo absoluto em depois diminui para um mínimo local em aumenta para um máximo local em e finalmente desce para um mínimo absoluto em
- Essa função deve ser contínua e suave, sem pontos de descontinuidade.
Passo 3
Agora podemos montar nosso gráfico!!
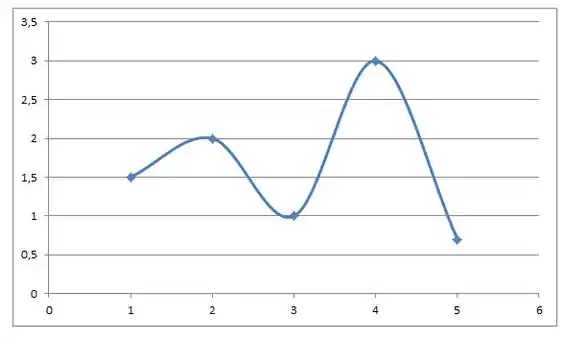
Prontinho!
Resposta
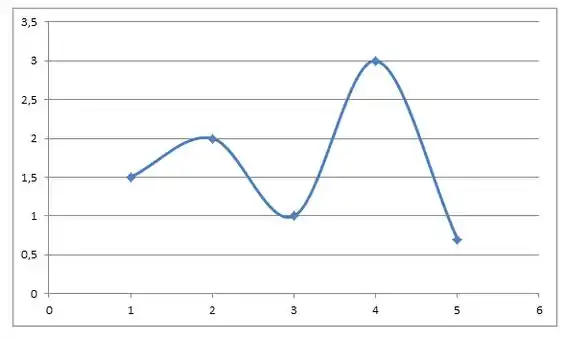 Vide a explicação.
Vide a explicação.