Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.2 - Ex. 2
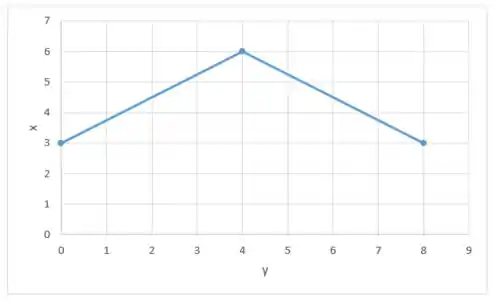
Desenhe o gráfico da função definida em [0, 8] que tenha e que a função não satisfaça à conclusão do teorema de Rolle em [0, 8].
Passo 1
Opa! Bora pra mais uma questão?! Ela pede pra a gente desenhar o gráfico da função definida em [0, 8] que tenha , porém essa função não deve satisfazer a conclusão do teorema de Rolle em .
Bem, antes de qualquer coisa vamos relembrar a definição do teorema de Rolle.
“Sendo f a função que satisfaça às seguintes condições:
- é contínua no intervalo fechado de
- é diferenciável no intervalo aberto de );
Então há um númerono intervalo aberto onde ”
Bom, com o teorema fresquinho na nossa cabeça agora, vamos montar o nosso gráfico.
Passo 2
Como o enunciado pediu para que a conclusão do teorema de Rolle não fosse respeitada, então não podemos ter um ponto com derivada nula. Além disso a outra informação é: . Desenhando esses pontos:
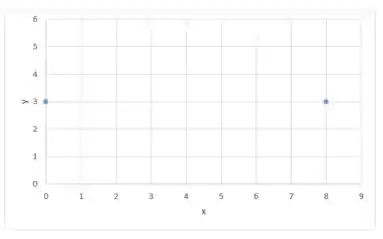
Olhando assim pode parecer que teremos uma parábola com concavidade pra baixo, assim por exemplo:
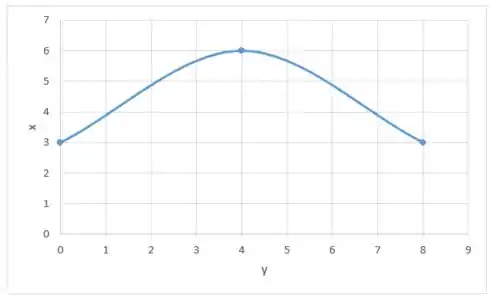
Mas nesse caso teríamos e estaríamos obedecendo a lei de Rolle! Não é o que queremos!
Passo 3
Outra possibilidade seria dizer que , nesse caso nosso gráfico seria apenas uma reta horizontal. Porém de novo . Então precisamos pensar...
Você pode reparar que o gráfico acima cresce suavemente até chagar a um ponto de máximo onde sua derivada é igual a zero e depois ele decresce suavemente de novo.
Mas e se tivéssemos uma “quina”?! Nesse caso não temos uma derivada definida! Logo não teremos !
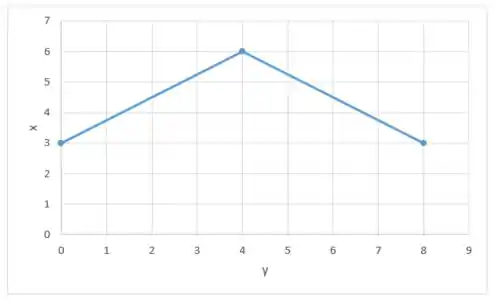
Repara que no lugar do “ponto máximo” temos uma mudança de direção abrupta, nesse caso podemos dizer que a nossa função não é contínua, portanto não podemos calcular sua derivada!
É claro que essa é apenas uma possibilidade, existem infinitas, inclusive:
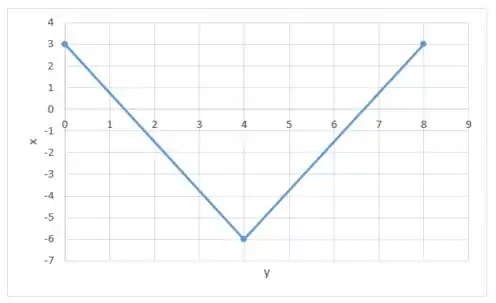
Fechou?!
Resposta
